Moyennes mobiles dans pandas

Introduction
Une moyenne mobile, également appelée moyenne glissante ou courante, est utilisée pour analyser les données de séries temporelles en calculant les moyennes de différents sous-ensembles de l’ensemble de données complet. Comme elle implique de prendre la moyenne de l’ensemble de données au fil du temps, elle est également appelée moyenne mobile (MM) ou moyenne roulante.
Il existe différentes façons de calculer la moyenne roulante, mais l’une d’entre elles consiste à prendre un sous-ensemble fixe d’une série complète de chiffres. La première moyenne mobile est calculée en faisant la moyenne du premier sous-ensemble fixe de nombres, puis le sous-ensemble est modifié en avançant vers le sous-ensemble fixe suivant (en incluant la valeur future dans le sous-groupe tout en excluant le nombre précédent de la série).
La moyenne mobile est surtout utilisée avec des données de séries chronologiques pour capturer les fluctuations à court terme tout en se concentrant sur les tendances plus longues.
Quelques exemples de données de séries temporelles peuvent être les prix des actions, les rapports météorologiques, la qualité de l’air, le produit intérieur brut, l’emploi, etc.
En général, la moyenne mobile lisse les données.
La moyenne mobile est une colonne vertébrale de nombreux algorithmes, et l’un de ces algorithmes est le modèle de moyenne mobile intégrée autorégressive (ARIMA), qui utilise les moyennes mobiles pour faire des prédictions sur les données de séries chronologiques.
Il existe différents types de moyennes mobiles :
-
Moyenne mobile simple (SMA) : La moyenne mobile simple (SMA) utilise une fenêtre glissante pour prendre la moyenne sur un nombre déterminé de périodes. Il s’agit d’une moyenne équipondérée des n données précédentes.
Pour mieux comprendre la SMA, prenons un exemple, une séquence de n valeurs :

alors la moyenne mobile équipondérée pour n points de données sera essentiellement la moyenne des M points de données précédents, où M est la taille de la fenêtre coulissante :

De même, pour le calcul des valeurs successives de la moyenne mobile, une nouvelle valeur sera ajoutée à la somme, et la valeur de la période précédente sera éliminée, puisque vous avez la moyenne des périodes précédentes, donc la somme complète à chaque fois n’est pas nécessaire :

- Moyenne mobile cumulative (CMA) : Contrairement à la moyenne mobile simple qui laisse tomber l’observation la plus ancienne au fur et à mesure que la nouvelle s’ajoute, la moyenne mobile cumulative prend en compte toutes les observations antérieures. La CMA n’est pas une très bonne technique pour analyser les tendances et lisser les données. La raison en est qu’elle fait la moyenne de toutes les données précédentes jusqu’au point de données actuel, donc une moyenne également pondérée de la séquence de n valeurs :



- Moyenne mobile exponentielle (EMA) : Contrairement à la SMA et la CMA, la moyenne mobile exponentielle donne plus de poids aux prix récents et en conséquence de quoi, elle peut être un meilleur modèle ou mieux capturer le mouvement de la tendance d’une manière plus rapide. La réaction de l’EMA est directement proportionnelle au modèle des données.
Puisque les EMA donnent un poids plus élevé sur les données récentes que sur les données plus anciennes, elles sont plus réactives aux derniers changements de prix par rapport aux SMA, ce qui rend les résultats des EMA plus opportuns et donc les EMA sont plus préférées aux autres techniques.
Assez de théorie, n’est-ce pas ? Sautons à la mise en œuvre pratique de la moyenne mobile.
Mise en œuvre de la moyenne mobile sur des données de séries temporelles
Moyenne mobile simple (SMA)
D’abord, créons des données de séries temporelles fictives et essayons de mettre en œuvre la SMA en utilisant seulement Python.
Supposons qu’il y a une demande pour un produit et qu’elle est observée pendant 12 mois (1 an), et vous devez trouver des moyennes mobiles pour des périodes de fenêtre de 3 et 4 mois.
Module d’importation
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| mois | demande | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Calculons la SMA pour une taille de fenêtre de 3, ce qui signifie que vous allez considérer trois valeurs à chaque fois pour calculer la moyenne mobile, et pour chaque nouvelle valeur, la valeur la plus ancienne sera ignorée.
Pour mettre en œuvre cela, vous utiliserez la fonction pandas iloc, puisque la colonne demand est ce dont vous avez besoin, vous fixerez la position de celle-ci dans la fonction iloc tandis que la ligne sera une variable i que vous continuerez à itérer jusqu’à ce que vous atteigniez la fin de la dataframe.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| mois | demande | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Pour un contrôle de bon sens, utilisons également la fonction pandas intégrée rolling et voyons si elle correspond à notre moyenne mobile simple personnalisée basée sur python.
df = df.iloc.rolling(window=3).mean()df.head()| mois | demande | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, donc comme vous pouvez le voir, les moyennes mobiles personnalisées et pandas correspondent exactement, ce qui signifie que votre implémentation de la SMA était correcte.
Calculons aussi rapidement la moyenne mobile simple pour une window_size de 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| mois | demande | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| mois | demande | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299,333333 | 289,5 | 289,5 |
Maintenant, vous allez tracer les données des moyennes mobiles que vous avez calculées.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>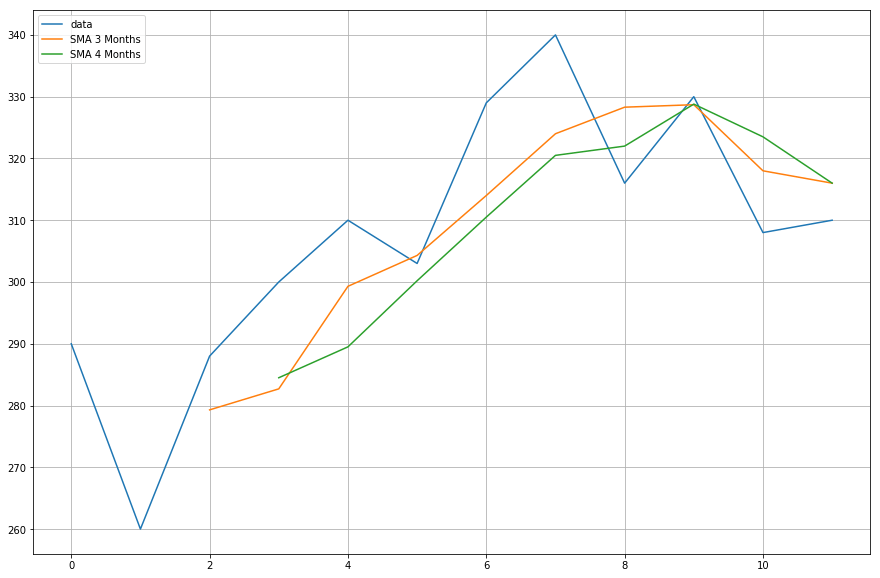
Moyenne mobile cumulative
Je pense que nous sommes maintenant prêts à passer à un ensemble de données réelles.
Pour la moyenne mobile cumulative, utilisons un air quality dataset qui peut être téléchargé à partir de ce lien.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Heure | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Le prétraitement est une étape essentielle dès que l’on travaille avec des données. Pour les données numériques, l’une des étapes de prétraitement les plus courantes consiste à vérifier la présence de valeurs NaN (Null). S’il y a des valeurs NaN, vous pouvez les remplacer par 0 ou par une moyenne ou par des valeurs précédentes ou successives ou même les laisser tomber. Bien que le remplacement soit normalement un meilleur choix que l’abandon, puisque cet ensemble de données a peu de valeurs NULL, l’abandon n’affectera pas la continuité de la série.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64D’après la sortie ci-dessus, vous pouvez observer qu’il y a environ 114 valeurs NaN à travers toutes les colonnes, cependant vous comprendrez qu’elles sont toutes à la fin de la série temporelle, donc abandonnons-les rapidement.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Vous allez appliquer la moyenne mobile cumulative sur le Temperature column (T), donc séparons rapidement cette colonne des données complètes.
df_T = pd.DataFrame(df.iloc)df_T.head()
Maintenant, vous allez utiliser la méthode pandas expanding pour trouver la moyenne cumulée des données ci-dessus. Si vous vous souvenez de l’introduction, contrairement à la moyenne mobile simple, la moyenne mobile cumulative considère toutes les valeurs précédentes lors du calcul de la moyenne.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Les données de séries temporelles sont tracées par rapport à l’heure, alors combinons la colonne de date et d’heure et convertissons-la en un objet datetime. Pour ce faire, vous utiliserez le module datetime de python (Source : Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Changeons l’indice du dataframe temperature avec datetime.
df_T.index = df.DateTimeTraçons maintenant la température réelle et la moyenne mobile cumulative par rapport au temps.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Moyenne mobile exponentielle
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DateTime | |||
| 2004-03-10 18 :00:00 | 13.6 | NaN | 13,600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12,20 | 13,274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>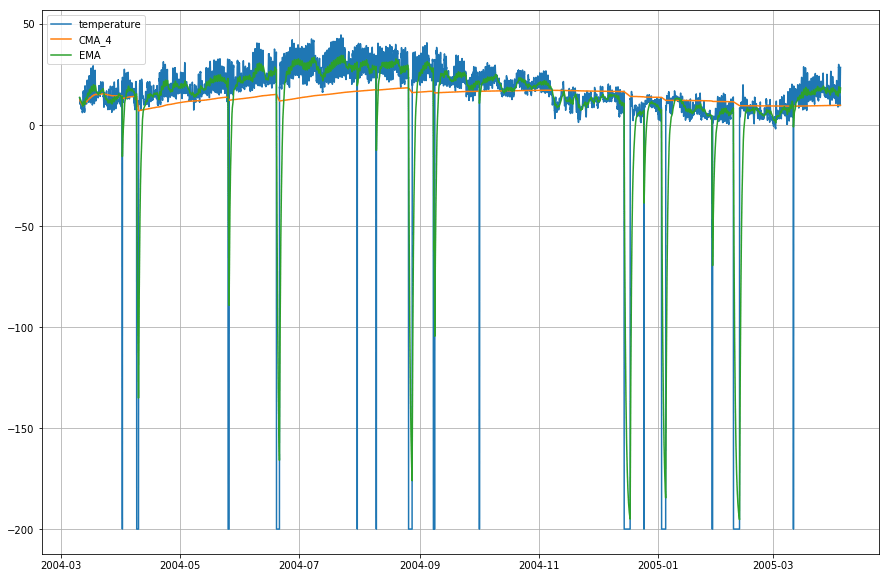
Wow ! Donc, comme vous pouvez l’observer dans le graphique ci-dessus, que le Exponential Moving Average (EMA) fait un superbe travail pour capturer le modèle des données tandis que le Cumulative Moving Average (CMA) manque par une marge considérable.
Aller plus loin!
Félicitations pour avoir terminé le tutoriel.
Ce tutoriel était un bon point de départ sur la façon dont vous pouvez calculer les moyennes mobiles de vos données et leur donner un sens.
Essayez d’écrire le code python de la moyenne mobile cumulative et exponentielle sans utiliser la bibliothèque pandas. Cela vous donnera une connaissance beaucoup plus approfondie de la façon dont elles sont calculées et en quoi elles sont différentes les unes des autres.
Il y a encore beaucoup à expérimenter. Essayez de calculer l’auto-corrélation partielle entre les données d’entrée et la moyenne mobile, et essayez de trouver une certaine relation entre les deux.
Si vous souhaitez en savoir plus sur les DataFrames dans pandas, suivez le cours interactif pandas Foundations de DataCamp.