Le dé-multiplexeur est un circuit combinatoire qui effectue l’opération inverse du multiplexeur. Il possède une seule entrée, ‘n’ lignes de sélection et un maximum de 2n sorties. L’entrée sera connectée à une de ces sorties en fonction des valeurs des lignes de sélection.

Puisqu’il y a ‘n’ lignes de sélection, il y aura 2n combinaisons possibles de zéros et de uns. Donc, chaque combinaison ne peut sélectionner qu’une seule sortie. Le démultiplexeur est aussi appelé De-Mux.

1×4 De-Multiplexeur

1×4 De-Multiplexeur a une entrée I, deux lignes de sélection, s1 & s0 et quatre sorties Y3, Y2, Y1 &Y0. Le schéma fonctionnel du dé-multiplexeur 1×4 est présenté dans la figure suivante.

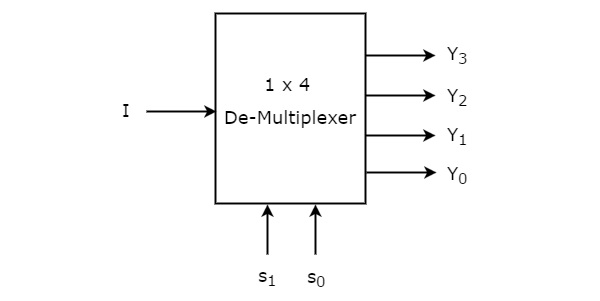
L’entrée unique ‘I’ sera connectée à l’une des quatre sorties, Y3 à Y0 en fonction des valeurs des lignes de sélection s1 & s0. La table de vérité du dé-multiplexeur 1×4 est présentée ci-dessous.

.

Entrées de sélection		Sorties
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	I
0	1	0	0	I	0
1	0	0	I	0	0
1	1	I	0	0	0	0

D’après la table de vérité ci-dessus, nous pouvons écrire directement les fonctions booléennes pour chaque sortie comme

$Y_{3}=s_{1}s_{0}}I$$

$Y_{2}=s_{1}{s_{0}}’I$$

$Y_{1}={s_{1}}’s_{0}I$$

$Y_{0}={s_1}'{s_{0}}’I$$

Nous pouvons implémenter ces fonctions booléennes en utilisant des inverseurs & 3-portes ET à trois entrées. Le schéma de circuit du dé-multiplexeur 1×4 est présenté dans la figure suivante.

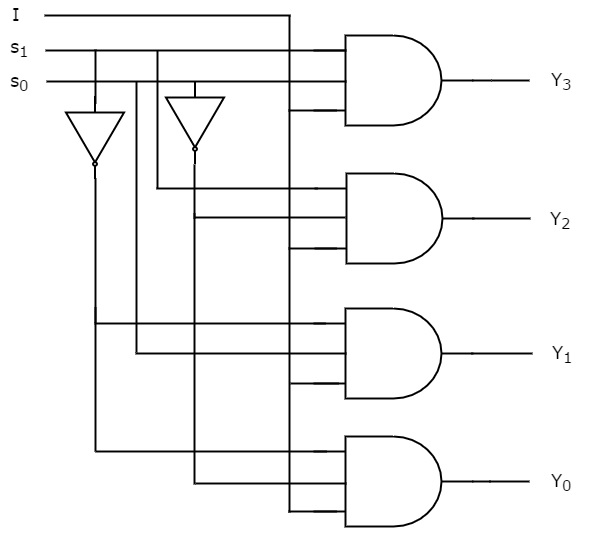
Nous pouvons facilement comprendre le fonctionnement du circuit ci-dessus. De même, vous pouvez implémenter le dé-multiplexeur 1×8 et le dé-multiplexeur 1×16 en suivant la même procédure.

Implémentation des dé-multiplexeurs d’ordre supérieur

Maintenant, implémentons les deux dé-multiplexeurs d’ordre supérieur suivants en utilisant des dé-multiplexeurs d’ordre inférieur.

• Dé-Multiplexeur 1×8
• Dé-Multiplexeur 1×16

Dé-Multiplexeur 1×8

Dans cette section, implémentons le Dé-Multiplexeur 1×8 en utilisant les Dé-Multiplexeurs 1×4 et le Dé-Multiplexeur 1×2. Nous savons que le De-Multiplexeur 1×4 a une seule entrée, deux lignes de sélection et quatre sorties. Alors que, le De-Multiplexeur 1×8 a une seule entrée, trois lignes de sélection et huit sorties.

Donc, nous avons besoin de deux De-Multiplexeurs 1×4 dans le deuxième étage afin d’obtenir les huit sorties finales. Puisque, le nombre d’entrées dans le deuxième étage est de deux, nous avons besoin de 1×2 DeMultiplexeur dans le premier étage afin que les sorties du premier étage seront les entrées du deuxième étage. L’entrée de ce dé-multiplexeur 1×2 sera l’entrée globale du dé-multiplexeur 1×8.

Disons que le dé-multiplexeur 1×8 a une entrée I, trois lignes de sélection s2, s1 & s0 et des sorties Y7 à Y0. La table de vérité du dé-multiplexeur 1×8 est présentée ci-dessous.

.

Entrées de sélection			Sorties
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

Nous pouvons implémenter le 1×8 De-Multiplexeur en utilisant des multiplexeurs d’ordre inférieur facilement en considérant la table de vérité ci-dessus. Le schéma fonctionnel du De-Multiplexeur 1×8 est présenté dans la figure suivante.

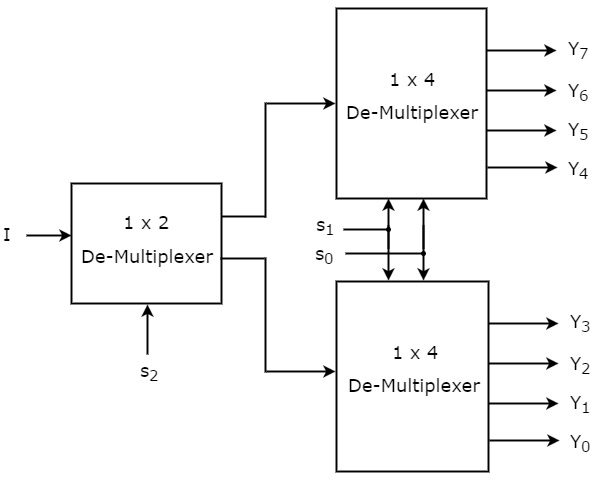
Les lignes de sélection communes, s1 & s0 sont appliquées aux deux 1×4 De-Multiplexeurs. Les sorties du De-Multiplexeur 1×4 supérieur sont Y7 à Y4 et les sorties du De-Multiplexeur 1×4 inférieur sont Y3 à Y0.

L’autre ligne de sélection, s2 est appliquée au De-Multiplexeur 1×2. Si s2 est zéro, alors une des quatre sorties du De-Multiplexeur 1×4 inférieur sera égale à l’entrée, I basée sur les valeurs des lignes de sélection s1 & s0. De même, si s2 est égal à un, alors l’une des quatre sorties du DeMultiplexeur 1×4 supérieur sera égale à l’entrée, I en fonction des valeurs des lignes de sélection s1 & s0.

1×16 De-Multiplexeur

Dans cette section, mettons en œuvre le De-Multiplexeur 1×16 en utilisant les De-Multiplexeurs 1×8 et le De-Multiplexeur 1×2. Nous savons que le De-Multiplexeur 1×8 a une seule entrée, trois lignes de sélection et huit sorties. Alors que, le De-Multiplexeur 1×16 a une seule entrée, quatre lignes de sélection et seize sorties.

Donc, nous avons besoin de deux De-Multiplexeurs 1×8 dans le deuxième étage afin d’obtenir les seize sorties finales. Puisque, le nombre d’entrées dans le deuxième étage est de deux, nous avons besoin d’un DeMultiplexeur 1×2 dans le premier étage afin que les sorties du premier étage soient les entrées du deuxième étage. L’entrée de ce Dé-Multiplexeur 1×2 sera l’entrée globale du Dé-Multiplexeur 1×16.

Disons que le Dé-Multiplexeur 1×16 a une entrée I, quatre lignes de sélection s3, s2, s1 & s0 et des sorties Y15 à Y0. Le schéma fonctionnel du démultiplexeur 1×16 utilisant des multiplexeurs d’ordre inférieur est présenté dans la figure suivante.

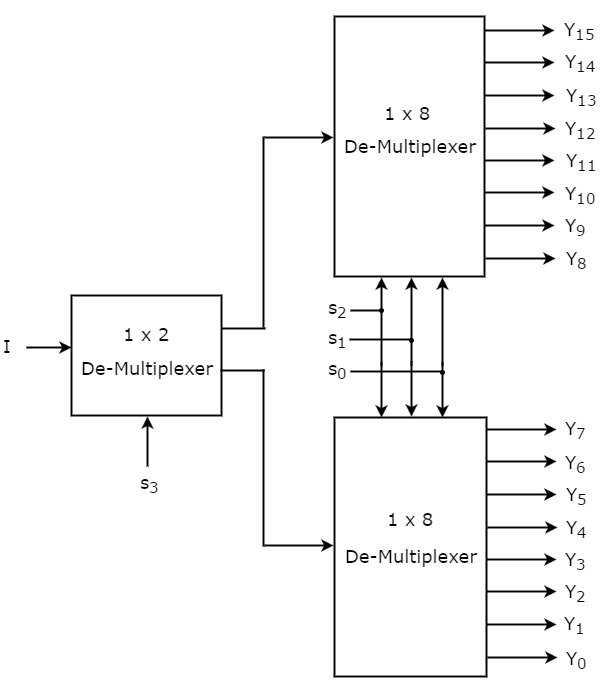
Les lignes de sélection communes s2, s1 & s0 sont appliquées aux deux démultiplexeurs 1×8. Les sorties du démultiplexeur 1×8 supérieur sont Y15 à Y8 et les sorties du démultiplexeur 1×8 inférieur sont Y7 à Y0.

L’autre ligne de sélection, s3 est appliquée au dé-multiplexeur 1×2. Si s3 est zéro, alors l’une des huit sorties du démultiplexeur inférieur 1×8 sera égale à l’entrée, I en fonction des valeurs des lignes de sélection s2, s1 & s0. De même, si s3 est égal à un, alors l’une des 8 sorties du démultiplexeur 1×8 supérieur sera égale à l’entrée, I sur la base des valeurs des lignes de sélection s2, s1 & s0.

.