MCDM ou MCDA sont des acronymes bien connus pour désigner la prise de décision à critères multiples et l’analyse décisionnelle multicritères ; Stanley Zionts a contribué à populariser l’acronyme avec son article de 1979 « MCDM – If not a Roman Numeral, then What ? », destiné à un public d’entrepreneurs.

MCDM s’intéresse à la structuration et à la résolution de problèmes de décision et de planification impliquant des critères multiples. L’objectif est de soutenir les décideurs confrontés à de tels problèmes. Typiquement, il n’existe pas une solution optimale unique pour de tels problèmes et il est nécessaire d’utiliser les préférences des décideurs pour différencier les solutions.

« Résoudre » peut être interprété de différentes manières. Il pourrait correspondre au choix de la « meilleure » alternative parmi un ensemble d’alternatives disponibles (où « meilleure » peut être interprété comme « l’alternative la plus préférée » d’un décideur). Une autre interprétation de « résoudre » pourrait consister à choisir un petit ensemble de bonnes alternatives, ou à regrouper les alternatives en différents ensembles de préférences. Une interprétation extrême pourrait être de trouver toutes les alternatives « efficaces » ou « non dominées » (que nous définirons prochainement).

La difficulté du problème provient de la présence de plus d’un critère. Il n’y a plus de solution optimale unique à un problème de MCDM qui puisse être obtenue sans intégrer d’information sur les préférences. Le concept de solution optimale est souvent remplacé par l’ensemble des solutions non dominées. Une solution est dite non dominée s’il n’est pas possible de l’améliorer pour un critère quelconque sans la sacrifier pour un autre. Par conséquent, il est logique pour le décideur de choisir une solution parmi l’ensemble des solutions non dominées. Sinon, il pourrait faire mieux pour certains ou tous les critères, et ne faire pire pour aucun d’entre eux. En général, cependant, l’ensemble des solutions non dominées est trop grand pour être présenté au décideur pour le choix final. Nous avons donc besoin d’outils qui aident le décideur à se concentrer sur les solutions (ou alternatives) préférées. Normalement, on doit  » troquer  » certains critères pour d’autres.

La GCDM est un domaine de recherche actif depuis les années 1970. Il existe plusieurs organisations liées au MCDM, notamment la Société internationale sur la prise de décision multicritères, l’Euro Working Group on MCDA et la section INFORMS sur le MCDM. Pour un historique, voir : Köksalan, Wallenius et Zionts (2011).Le MCDM fait appel à des connaissances dans de nombreux domaines, notamment :

• Mathématiques
• Analyse de la décision
• Économie
• Technologie informatique
• Génie logiciel
• Systèmes d’information

Une typologieEdit

Il existe différentes classifications des problèmes et des méthodes de GCDM. Une distinction majeure entre les problèmes de GCDM repose sur le fait que les solutions sont définies explicitement ou implicitement.

• Problèmes d’évaluation multicritères : Ces problèmes consistent en un nombre fini d’alternatives, explicitement connues au début du processus de solution. Chaque alternative est représentée par sa performance dans plusieurs critères. Le problème peut être défini comme la recherche de la meilleure alternative pour un décideur (DM), ou la recherche d’un ensemble de bonnes alternatives. On peut également s’intéresser au « tri » ou à la « classification » des alternatives. Le tri consiste à placer les alternatives dans un ensemble de classes ordonnées en fonction des préférences (comme l’attribution de notes de crédit aux pays), et la classification consiste à affecter les alternatives à des ensembles non ordonnés (comme le diagnostic des patients en fonction de leurs symptômes). Certaines des méthodes MCDM de cette catégorie ont été étudiées de manière comparative dans le livre de Triantaphyllou sur ce sujet, 2000.
• Les problèmes de conception à critères multiples (problèmes de programmation mathématique à objectifs multiples) : Dans ces problèmes, les alternatives ne sont pas explicitement connues. Une alternative (solution) peut être trouvée en résolvant un modèle mathématique. Le nombre d’alternatives est soit infini (dénombrable ou non) soit fini, mais typiquement exponentiellement grand (dans le nombre de variables s’étendant sur des domaines finis.)

Qu’il s’agisse d’un problème d’évaluation ou d’un problème de conception, l’information sur les préférences des DM est nécessaire pour différencier les solutions. Les méthodes de solution des problèmes MCDM sont communément classées en fonction du moment où l’information de préférence est obtenue du DM.

Il existe des méthodes qui nécessitent l’information de préférence du DM au début du processus, transformant le problème en un problème essentiellement à critère unique. On dit de ces méthodes qu’elles fonctionnent par « articulation préalable des préférences ». Les méthodes basées sur l’estimation d’une fonction de valeur ou sur le concept de « relations de surclassement », le processus de hiérarchie analytique et certaines méthodes basées sur des règles de décision tentent de résoudre les problèmes d’évaluation à critères multiples en utilisant l’articulation préalable des préférences. De même, il existe des méthodes développées pour résoudre les problèmes de conception à critères multiples en utilisant l’articulation préalable des préférences par la construction d’une fonction de valeur. La plus connue de ces méthodes est sans doute la programmation par objectifs. Une fois la fonction de valeur construite, le programme mathématique à objectif unique qui en résulte est résolu pour obtenir une solution préférée.

Certaines méthodes requièrent des informations sur les préférences du DM tout au long du processus de solution. On parle alors de méthodes interactives ou de méthodes qui nécessitent une « articulation progressive des préférences ». Ces méthodes ont été bien développées à la fois pour l’évaluation multicritères (voir par exemple Geoffrion, Dyer et Feinberg, 1972, et Köksalan et Sagala, 1995 ) et pour les problèmes de conception (voir Steuer, 1986).

Les problèmes de conception multicritères nécessitent généralement la résolution d’une série de modèles de programmation mathématique afin de révéler des solutions implicitement définies. Pour ces problèmes, une représentation ou une approximation des « solutions efficaces » peut également présenter un intérêt. Cette catégorie est appelée « articulation postérieure des préférences », ce qui implique que l’implication du SM commence postérieurement à la révélation explicite de solutions « intéressantes » (voir par exemple Karasakal et Köksalan, 2009).

Lorsque les modèles de programmation mathématique contiennent des variables entières, les problèmes de conception deviennent plus difficiles à résoudre. L’optimisation combinatoire multiobjectif (MOCO) constitue une catégorie spéciale de ces problèmes posant des difficultés de calcul substantielles (voir Ehrgott et Gandibleux, 2002, pour une revue).

Représentations et définitionsModification

Le problème de MCDM peut être représenté dans l’espace des critères ou l’espace des décisions. Alternativement, si différents critères sont combinés par une fonction linéaire pondérée, il est également possible de représenter le problème dans l’espace des poids. Vous trouverez ci-dessous les démonstrations des espaces des critères et des poids ainsi que quelques définitions formelles.

Représentation de l’espace des critèresEdit

Supposons que nous évaluons les solutions dans une situation de problème spécifique en utilisant plusieurs critères. Supposons en outre que plus est meilleur pour chaque critère. Alors, parmi toutes les solutions possibles, nous sommes idéalement intéressés par les solutions qui sont performantes dans tous les critères considérés. Cependant, il est peu probable qu’une seule solution soit performante pour tous les critères considérés. En général, certaines solutions sont performantes pour certains critères et d’autres pour d’autres. Trouver un moyen de faire des compromis entre les critères est l’un des principaux efforts de la littérature MCDM.

Mathématiquement, le problème MCDM correspondant aux arguments ci-dessus peut être représenté comme

« max » q sous réserve que q ∈ Q

où q est le vecteur de k fonctions de critère (fonctions objectives) et Q est l’ensemble réalisable, Q ⊆ Rk.

Si Q est défini explicitement (par un ensemble d’alternatives), le problème résultant est appelé un problème d’évaluation multicritère.

Si Q est défini implicitement (par un ensemble de contraintes), le problème résultant est appelé un problème de conception multicritère.

Les guillemets sont utilisés pour indiquer que la maximisation d’un vecteur n’est pas une opération mathématique bien définie. Cela correspond à l’argument selon lequel nous devrons trouver un moyen de résoudre le compromis entre les critères (typiquement basé sur les préférences d’un décideur) lorsqu’une solution performante pour tous les critères n’existe pas.

Représentation de l’espace de décisionEdit

L’espace de décision correspond à l’ensemble des décisions possibles qui s’offrent à nous. Les valeurs des critères seront des conséquences des décisions que nous prenons. Par conséquent, nous pouvons définir un problème correspondant dans l’espace de décision. Par exemple, lors de la conception d’un produit, nous décidons des paramètres de conception (variables de décision) dont chacun affecte les mesures de performance (critères) avec lesquelles nous évaluons notre produit.

Mathématiquement, un problème de conception à critères multiples peut être représenté dans l’espace de décision comme suit :

max q = f ( x ) = f ( x 1 , … , x n ) sous réserve que q ∈ Q = { f ( x ) : x ∈ X , X ⊆ R n }. {\displaystyle {\begin{aligned}\max q&=f(x)=f(x_{1},\ldots ,x_{n})\{\text{subject to}\q\in Q&={f(x):x\in X,\,X\subseteq \mathbb {R} ^{n}}\}end{aligned}}}

où X est l’ensemble réalisable et x est le vecteur de variables de décision de taille n.

Un cas particulier bien développé est obtenu lorsque X est un polyèdre défini par des inégalités et des égalités linéaires. Si toutes les fonctions objectives sont linéaires en termes de variables de décision, cette variation conduit à la programmation linéaire à objectifs multiples (MOLP), une sous-classe importante de problèmes de MCDM.

Il existe plusieurs définitions qui sont centrales en MCDM. Deux définitions étroitement liées sont celles de la nondominance (définie à partir de la représentation de l’espace des critères) et de l’efficacité (définie à partir de la représentation de la variable de décision).

Définition 1. q* ∈ Q est nondominée s’il n’existe pas un autre q ∈ Q tel que q ≥ q* et q ≠ q*.

En gros, une solution est nondominée tant qu’elle n’est pas inférieure à toute autre solution disponible dans tous les critères considérés.

Définition 2. x* ∈ X est efficace s’il n’existe pas un autre x ∈ X tel que f(x) ≥ f(x*) et f(x) ≠ f(x*).

Si un problème MCDM représente bien une situation de décision, alors la solution la plus préférée d’un DM doit être une solution efficace dans l’espace de décision, et son image est un point nondominant dans l’espace des critères. Les définitions suivantes sont également importantes.

Définition 3. q* ∈ Q est faiblement nondominée s’il n’existe pas un autre q ∈ Q tel que q > q*.

Définition 4. x* ∈ X est faiblement efficace s’il n’existe pas un autre x ∈ X tel que f(x) > f(x*).

Les points faiblement non dominés comprennent tous les points non dominés et certains points dominés spéciaux. L’importance de ces points dominés spéciaux vient du fait qu’ils apparaissent couramment dans la pratique et qu’une attention particulière est nécessaire pour les distinguer des points non dominés. Si, par exemple, nous maximisons un seul objectif, nous pouvons nous retrouver avec un point faiblement nondominé qui est dominé. Les points dominés de l’ensemble faiblement non dominé sont situés soit sur des plans verticaux ou horizontaux (hyperplans) dans l’espace des critères.

Point idéal : (dans l’espace des critères) représente le meilleur (le maximum pour les problèmes de maximisation et le minimum pour les problèmes de minimisation) de chaque fonction objectif et correspond généralement à une solution infaisable.

Point nadir : (dans l’espace des critères) représente le pire (le minimum pour les problèmes de maximisation et le maximum pour les problèmes de minimisation) de chaque fonction objectif parmi les points de l’ensemble non dominé et correspond typiquement à un point dominé.

Le point idéal et le point nadir sont utiles au SM pour avoir la « sensation » de la gamme de solutions (bien qu’il ne soit pas simple de trouver le point nadir pour les problèmes de conception ayant plus de deux critères).

Illustrations des espaces de décision et de critèresEdit

Le problème MOLP à deux variables suivant dans l’espace des variables de décision aidera à démontrer certains des concepts clés graphiquement.

Figure 1. Démonstration de l’espace de décision

max f 1 ( x ) = – x 1 + 2 x 2 max f 2 ( x ) = 2 x 1 – x 2 sous réserve de x 1 ≤ 4 x 2 ≤ 4 x 1 + x 2 ≤ 7 – x 1 + x 2 ≤ 3 x 1 – x 2 ≤ 3 x 1 , x 2 ≥ 0 {\displaystyle {\begin{aligned}\max f_{1}(\mathbf {x} )&=-x_{1}+2x_{2}\\\\\\\max f_{2}(\mathbf {x} )&=2x_{1}-x_{2}\{\text{subject to}\x_{1}&\leq 4\\x_{2}&\leq 4\x_{1}+x_{2}&\leq 7\\x_{1}+x_{2}&\leq 3\x_{1}-x_{2}&\leq 3\x_{1},x_{2}&\geq 0\end{aligned}}}

Dans la figure 1, les points extrêmes « e » et « b » maximisent respectivement le premier et le second objectif. La frontière rouge entre ces deux points extrêmes représente l’ensemble efficace. On peut voir sur la figure que, pour toute solution réalisable en dehors de l’ensemble efficace, il est possible d’améliorer les deux objectifs par certains points de l’ensemble efficace. Inversement, pour tout point de l’ensemble efficace, il n’est pas possible d’améliorer les deux objectifs en passant à une autre solution réalisable. A ces solutions, on doit sacrifier d’un des objectifs afin d’améliorer l’autre objectif.

En raison de sa simplicité, le problème ci-dessus peut être représenté dans l’espace des critères en remplaçant les x par les f ‘s comme suit :

Figure 2. Démonstration des solutions dans l’espace des critères

Max f1 Max f2 soumis à f1 + 2f2 ≤ 12 2f1 + f2 ≤ 12 f1 + f2 ≤ 7 f1 – f2 ≤ 9 -f1 + f2 ≤ 9 f1 + 2f2 ≥ 0 2f1 + f2 ≥ 0

Nous présentons l’espace des critères graphiquement dans la figure 2. Il est plus facile de détecter les points non dominés (correspondant aux solutions efficaces dans l’espace de décision) dans l’espace des critères. La région nord-est de l’espace réalisable constitue l’ensemble des points non dominés (pour les problèmes de maximisation).

Génération de solutions non dominéesModification

Il existe plusieurs façons de générer des solutions non dominées. Nous allons en aborder deux. La première approche peut générer une classe spéciale de solutions non dominées alors que la seconde approche peut générer n’importe quelle solution non dominée.

• Sommes pondérées (Gass & Saaty, 1955)

Si nous combinons les critères multiples en un seul critère en multipliant chaque critère par un poids positif et en additionnant les critères pondérés, alors la solution au problème à critère unique résultant est une solution efficace spéciale. Ces solutions efficaces spéciales apparaissent aux points d’angle de l’ensemble des solutions disponibles. Les solutions efficaces qui ne se trouvent pas aux points d’angle ont des caractéristiques particulières et cette méthode n’est pas capable de trouver de tels points. Mathématiquement, nous pouvons représenter cette situation comme

max wT.q = wT.f(x), w> 0 sous réserve que x ∈ X

En faisant varier les poids, les sommes pondérées peuvent être utilisées pour générer des solutions efficaces aux points extrêmes pour les problèmes de conception, et des points soutenus (convexes non dominés) pour les problèmes d’évaluation.

• Fonction scalarisante de réalisation (Wierzbicki, 1980)

Figure 3. Projection de points sur l’ensemble non dominé avec une fonction de scalarisation de l’accomplissement

Les fonctions de scalarisation de l’accomplissement combinent également plusieurs critères en un seul en les pondérant d’une manière très particulière. Elles créent des contours rectangulaires s’éloignant d’un point de référence vers les solutions efficaces disponibles. Cette structure spéciale permet aux fonctions de scalarisation des réalisations d’atteindre n’importe quelle solution efficace. C’est une propriété puissante qui rend ces fonctions très utiles pour les problèmes de MCDM.

Mathématiquement, nous pouvons représenter le problème correspondant comme

Min s(g, q, w, ρ) = Min {maxi + ρ ∑i (gi – qi)}, sous réserve que q ∈ Q

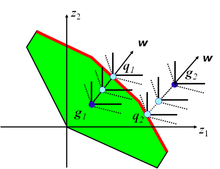
La fonction de scalarisation de l’accomplissement peut être utilisée pour projeter n’importe quel point (faisable ou infaisable) sur la frontière efficiente. Tout point (soutenu ou non) peut être atteint. Le deuxième terme de la fonction objectif est nécessaire pour éviter de générer des solutions inefficaces. La figure 3 montre comment un point réalisable, g1, et un point infaisable, g2, sont projetés sur les points non dominés, q1 et q2, respectivement, le long de la direction w en utilisant une fonction de scalarisation de l’accomplissement. Les contours en pointillés et en traits pleins correspondent aux contours de la fonction objectif avec et sans le second terme de la fonction objectif, respectivement.

Résolution des problèmes de MCDMEdit

Différentes écoles de pensée se sont développées pour résoudre les problèmes de MCDM (de type conception et évaluation). Pour une étude bibliométrique montrant leur développement dans le temps, voir Bragge, Korhonen, H. Wallenius et J. Wallenius .

École de programmation mathématique à objectifs multiples

(1) Maximisation vectorielle : Le but de la maximisation vectorielle est d’approcher l’ensemble non dominé ; développée à l’origine pour des problèmes de programmation linéaire à objectifs multiples (Evans et Steuer, 1973 ; Yu et Zeleny, 1975).

(2) Programmation interactive : Des phases de calcul alternent avec des phases de prise de décision (Benayoun et al, 1971 ; Geoffrion, Dyer et Feinberg, 1972 ; Zionts et Wallenius, 1976 ; Korhonen et Wallenius, 1988). Aucune connaissance explicite de la fonction de valeur du DM n’est supposée.

École de programmation par objectifs

Le but est de fixer des valeurs cibles apriori pour les objectifs, et de minimiser les écarts pondérés par rapport à ces objectifs. Les poids d’importance ainsi que les poids préemptifs lexicographiques ont été utilisés (Charnes et Cooper, 1961).

Théoriciens des ensembles flous

Les ensembles flous ont été introduits par Zadeh (1965) comme une extension de la notion classique d’ensembles. Cette idée est utilisée dans de nombreux algorithmes MCDM pour modéliser et résoudre les problèmes flous.

Théoriciens de l’utilité multi-attributs

Les fonctions d’utilité ou de valeur multi-attributs sont sollicitées et utilisées pour identifier l’alternative la plus préférée ou pour classer les alternatives. Des techniques d’entretien élaborées, qui existent pour éliciter des fonctions d’utilité additives linéaires et des fonctions d’utilité non linéaires multiplicatives, sont utilisées (Keeney et Raiffa, 1976).

École française

L’école française se concentre sur l’aide à la décision, en particulier la famille ELECTRE de méthodes de surclassement qui a vu le jour en France au milieu des années 1960. La méthode a été proposée pour la première fois par Bernard Roy (Roy, 1968).

École d’optimisation multiobjectif évolutionnaire (EMO)

Les algorithmes EMO commencent avec une population initiale, et la mettent à jour en utilisant des processus conçus pour imiter les principes naturels de survie du plus apte et les opérateurs de variation génétique pour améliorer la population moyenne d’une génération à l’autre. L’objectif est de converger vers une population de solutions qui représentent l’ensemble non dominé (Schaffer, 1984 ; Srinivas et Deb, 1994). Plus récemment, il y a des efforts pour incorporer des informations de préférence dans le processus de solution des algorithmes EMO (voir Deb et Köksalan, 2010).

Méthodes basées sur la théorie des systèmes gris

Dans les années 1980, Deng Julong a proposé la théorie des systèmes gris (GST) et son premier modèle de prise de décision à attributs multiples, appelé modèle d’analyse relationnelle grise (GRA) de Deng. Plus tard, les spécialistes des systèmes gris ont proposé de nombreuses méthodes basées sur la TPS, comme le modèle GRA absolu de Liu Sifeng, la prise de décision à cible grise (GTDM) et l’analyse décisionnelle absolue grise (GADA).

Processus de hiérarchie analytique (AHP)

L’AHP décompose d’abord le problème de décision en une hiérarchie de sous-problèmes. Ensuite, le décideur évalue l’importance relative de ses différents éléments par des comparaisons par paires. L’AHP convertit ces évaluations en valeurs numériques (poids ou priorités), qui sont utilisées pour calculer un score pour chaque alternative (Saaty, 1980). Un indice de cohérence mesure la mesure dans laquelle le décideur a été cohérent dans ses réponses. AHP est l’une des techniques les plus controversées énumérées ici, certains chercheurs de la communauté MCDA estimant qu’elle est imparfaite. Les mathématiques sous-jacentes sont également plus compliquées, bien qu’elle ait gagné une certaine popularité en raison des logiciels disponibles dans le commerce.

Plusieurs articles ont examiné l’application des techniques de MCDM dans diverses disciplines telles que le MCDM flou, le MCDM classique, l’énergie durable et renouvelable, la technique de l’AHP, les systèmes de transport, la qualité du service, la méthode TOPSIS, les problèmes de gestion de l’énergie, l’apprentissage en ligne, le tourisme et l’hospitalité, les méthodes SWARA et WASPAS.

Méthodes MCDMEdit

Les méthodes MCDM suivantes sont disponibles, dont beaucoup sont mises en œuvre par des logiciels spécialisés dans la prise de décision :

• Méthode de randomisation des indices agrégés (AIRM)
• Processus de hiérarchie analytique (AHP)
• Processus de réseau analytique (ANP)
• Processus de faisceau d’équilibre
• Méthode de base-.critère (BCM)
• Méthode du meilleur pire (BWM)
• Modèle Brown-Gibson
• Méthode des objets caractéristiques (COMET)
• Choosing By Advantages (CBA)
• Hiérarchie de valeur conjointe (CVA)
• Analyse d’enveloppement des données
• Expert de décision (DEX)
• Approches de désagrégation – agrégation (UTA*, UTAII, UTADIS)
• Ensemble brut (approche par ensemble brut)
• Approche par ensemble brut basée sur la dominance (DRSA)(DRSA)
• ELECTRE (Outranking)
• Evaluation basée sur la distance par rapport à la solution moyenne (EDAS)
• Approche de raisonnement probant (ER)
• Programmation par objectif (GP)
• Analyse relationnelle grise (GRA)
• Produit interne des vecteurs (IPV)
• Mesure de l’attractivité par une technique d’évaluation basée sur les catégories (MACBETH)
• Technique d’évaluation multi-attributs simple (SMART)
• .Attribute Rating Technique (SMART)
• Système de décision multicritères stratifié (SMCDM)
• Inférence globale de qualité multi-attribut (MAGIQ)
• Théorie de l’utilité multi-attribut (MAUT)
• Théorie de la valeur multi-attribut (MAVT)attributs (MAVT)
• Décision multicritères markovienne
• Nouvelle approche de l’évaluation (NATA)
• Système flou non structurel d’aide à la décision (NSFDSS)
• Potentiellement. All Pairwise RanKings of all possible Alternatives (PAPRIKA)
• PROMETHEE (Outranking)
• Ranking based on optimal points (RBOP)
• Analyse d’acceptabilité multicritères stochastique. (SMAA)
• Méthode de classement par supériorité et infériorité (méthode SIR)
• Technique d’ordre de priorité par similitude à la solution idéale (TOPSIS)
• Analyse de la valeur (VA)
• . Ingénierie de la valeur (VE)
• Méthode VIKOR
• Modèle de produit pondéré (WPM)
• Modèle de somme pondérée (WSM)
• Modelo Integrado de Valor para Estructuras Sostenibles (MIVES)

.