Liukuvat keskiarvot pandassa

Esittely
Liukuvaa keskiarvoa, jota kutsutaan myös liukuvaksi tai juoksevaksi keskiarvoksi, käytetään aikasarjadatan analysointiin laskemalla keskiarvoja koko tietokokonaisuuden eri osajoukoista. Koska siinä otetaan keskiarvo datajoukosta ajan kuluessa, sitä kutsutaan myös liukuvaksi keskiarvoksi (MM) tai liukuvaksi keskiarvoksi.
Liukuvan keskiarvon voi laskea eri tavoin, mutta yksi tällainen tapa on ottaa kiinteä osajoukko täydellisestä numerosarjasta. Ensimmäinen liukuva keskiarvo lasketaan laskemalla keskiarvo ensimmäisestä kiinteästä numeroiden osajoukosta, minkä jälkeen osajoukkoa muutetaan siirtymällä eteenpäin seuraavaan kiinteään osajoukkoon (sisällyttämällä tuleva arvo osajoukkoon ja jättämällä samalla edellinen numero pois sarjasta).
Liukuvaa keskiarvoa käytetään useimmiten aikasarjadatan kanssa lyhytaikaisten vaihteluiden taltioimiseksi samalla kun keskitytään pidempiin suuntauksiin.
Muutamia esimerkkejä aikasarjadatasta voivat olla pörssikurssit, säätiedotukset, ilmanlaatu, bruttokansantuote, työllisyys jne.
Yleisesti ottaen liukuva keskiarvo tasoittaa dataa.
Liukuva keskiarvo on monien algoritmien selkäranka, ja yksi tällainen algoritmi on Autoregressiivinen integroitu liukuvan keskiarvon malli (ARIMA), joka käyttää liukuvia keskiarvoja aikasarjadatan ennusteiden tekemiseen.
Liukuvia keskiarvoja on erityyppisiä:
-
Yksinkertainen liukuva keskiarvo (SMA, Simple Moving Average): Yksinkertainen liukuva keskiarvo (Simple Moving Average, SMA) käyttää liukuvaa ikkunaa keskiarvon ottamiseksi määrätyn määrän ajanjaksoja. Se on tasaisesti painotettu keskiarvo edellisestä n datasta.
Ymmärtääksemme SMA:ta tarkemmin, otetaan esimerkkinä n arvon jakso:

tällöin n datapisteen tasavertaisesti painotettu liukuva keskiarvo on pohjimmiltaan edellisten M datapisteen keskiarvo, jossa M on liukuvan ikkunan koko:

Vastaavasti seuraavia liukuvan keskiarvon arvoja laskettaessa summaan lisätään uusi arvo ja edellisen aikajakson arvo jätetään pois, koska käytössä on edellisten aikajaksojen keskiarvo, joten täyttä yhteenlaskua ei joka kerta tarvita:

- Kumulatiivinen liukuva keskiarvo (CMA): Toisin kuin yksinkertainen liukuva keskiarvo, joka poistaa vanhimman havainnon, kun uusi lisätään, kumulatiivinen liukuva keskiarvo ottaa huomioon kaikki aiemmat havainnot. CMA ei ole kovin hyvä tekniikka trendien analysointiin ja tietojen tasoittamiseen. Syynä on se, että se keskiarvoistaa kaikki aiemmat tiedot nykyiseen datapisteeseen asti, joten se on n arvon sarjan tasaisesti painotettu keskiarvo:



- Eksponentiaalinen liukuva keskiarvo (EMA): Toisin kuin SMA ja CMA, eksponentiaalinen liukuva keskiarvo antaa enemmän painoarvoa viimeaikaisille hinnoille, minkä seurauksena se voi olla parempi malli tai paremmin kaapata trendin liikkeen nopeammin. EMA:n reaktio on suoraan verrannollinen tietojen malliin.
Sen vuoksi, että EMA:t antavat suuremman painoarvon viimeisimmille tiedoille kuin vanhemmille tiedoille, ne reagoivat paremmin viimeisimpiin hinnanmuutoksiin verrattuna SMA:iin, mikä tekee EMA:n tuloksista ajantasaisempia, ja siksi EMA:ta suositaan enemmän kuin muita tekniikoita.
Ei nyt riitä teoriaa, eikö? Hyppäämme liukuvan keskiarvon käytännön toteutukseen.
Liukuvan keskiarvon toteuttaminen aikasarjadataan
Simppeli liukuva keskiarvo (SMA)
Luotaan ensin dummy-aikasarjadataa ja kokeillaan SMA:n toteuttamista pelkän Pythonin avulla.
Asetetaan, että tuotteelle on kysyntää ja sitä tarkkaillaan 12 kuukauden ajan (1 vuosi), ja sinun on löydettävä liukuvat keskiarvot 3 ja 4 kuukauden ikkuna-ajoille.
Import moduuli
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| kuukausi | kysyntä | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Lasketaan SMA ikkunakoolle 3, mikä tarkoittaa, että liukuvan keskiarvon laskennassa otetaan huomioon aina kolme arvoa, ja jokaisen uuden arvon kohdalla vanhinta arvoa ei oteta huomioon.
Toteuttaaksesi tämän, käytät pandan iloc-funktiota, koska demand-sarake on se, mitä tarvitset, kiinnität sen sijainnin iloc-funktiossa, kun taas rivi on muuttuja i, jota jatkat iterointia, kunnes saavutat dataframen loppuun.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| kuukausi | kysyntä | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Käytetään järkevyyden tarkistamiseksi myös pandas sisäänrakennettua rolling-funktiota ja katsotaan, täsmääkö se mukautetun python-pohjaisen yksinkertaisen liukuvan keskiarvon kanssa.
df = df.iloc.rolling(window=3).mean()df.head()| kuukausi | kysyntä | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.33333333 |
Cool, joten kuten huomaat, mukautetut ja Pandasin liukuvat keskiarvot vastaavat täsmälleen toisiaan, mikä tarkoittaa, että SMA:n toteutuksesi oli oikea.
Lasketaan myös nopeasti yksinkertainen liukuva keskiarvo window_size:lle 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| kuukausi | kysyntä | SMA_3 | pandas_SMA_3 | SMA_4 | ||
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | |
| 1 | 2 | 260 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| kuukausi | kysyntä | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN | |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN | |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 | 289.5 |
Nyt piirrät laskemiesi liukuvien keskiarvojen tiedot.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>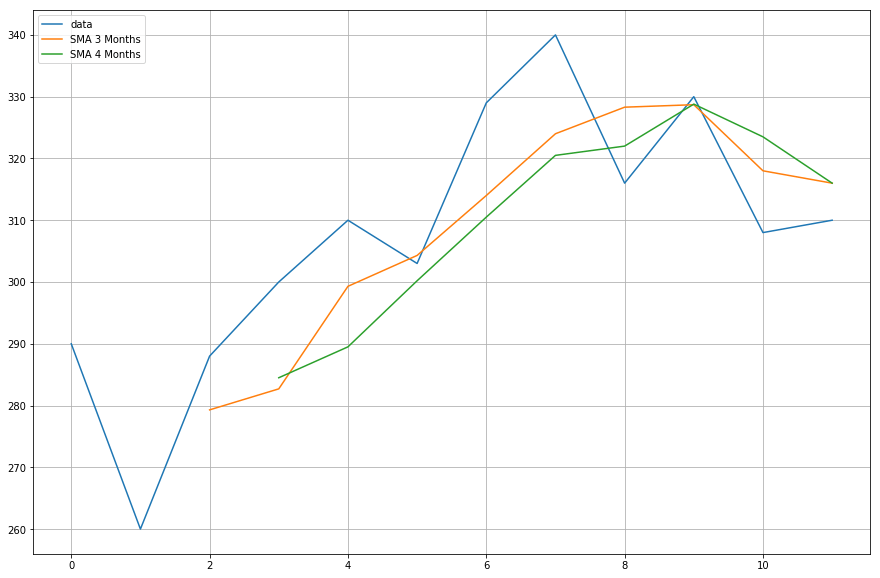
Kumulatiivinen liukuva keskiarvo
Luulempa, että olemme nyt valmiita siirtymään todelliseen aineistoon.
Kumulatiiviseen liukuvaan keskiarvoon käytämme air quality dataset, jonka voi ladata tästä linkistä.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Esikäsittely on olennainen vaihe aina, kun työskentelet datan kanssa. Numeeristen tietojen kohdalla yksi yleisimmistä esikäsittelyvaiheista on NaN (Null)-arvojen tarkistaminen. Jos NaN-arvoja on, voit korvata ne joko 0:lla tai keskiarvolla tai edeltävillä tai seuraavilla arvoilla tai jopa poistaa ne. Vaikka korvaaminen on yleensä parempi vaihtoehto kuin niiden pudottaminen, koska tässä tietokokonaisuudessa on vain vähän NULL-arvoja, niiden pudottaminen ei vaikuta sarjan jatkuvuuteen.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Yllä olevasta tulosteesta voit havaita, että NaN-arvoja on noin 114 kaikissa sarakkeissa, mutta tulet kuitenkin huomaamaan, että ne ovat kaikki aikasarjan lopussa, joten pudotetaan ne nopeasti.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Tulee soveltaa kumulatiivista liukuvaa keskiarvoa Temperature column (T), joten erotetaan tämä sarake nopeasti koko datasta. käytät pandas expanding -menetelmää löytääksesi edellä mainittujen tietojen kumulatiivisen keskiarvon. Jos muistat johdannosta, toisin kuin yksinkertaisessa liukuvassa keskiarvossa, kumulatiivisessa liukuvassa keskiarvossa otetaan keskiarvoa laskettaessa huomioon kaikki edeltävät arvot.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Aikasarjadataa piirretään ajan suhteen, joten yhdistetään päivämäärän ja kellonajan sarakkeet toisiinsa ja muunnetaan ne datetime-objektiksi. Tähän käytetään pythonin datetime-moduulia (Lähde: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Muutetaan temperature-datakehyksen indeksi datetime-olioksi.
df_T.index = df.DateTimePiirretään nyt todellisen lämpötilan ja kumulatiivisen liukuvan keskiarvon kuvaaja ajan suhteen.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Eksponentiaalinen liukuva keskiarvo
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | ||
|---|---|---|---|---|
| DateTime | ||||
| 2004-…03-10 18:00:00 | 13.6 | NaN | 13.600000 | |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 | |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 | |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>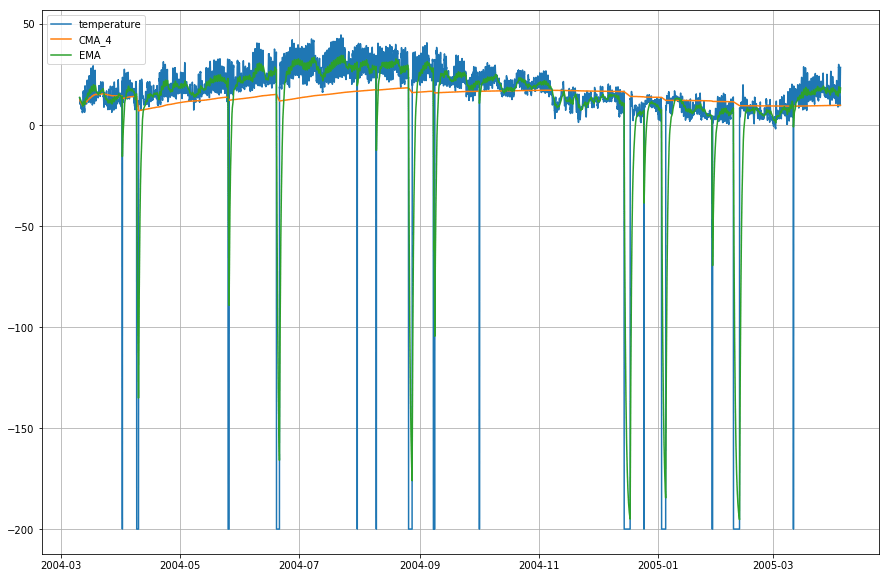
Vau! Kuten yllä olevasta kuvaajasta voi siis havaita, että Exponential Moving Average (EMA) tekee erinomaista työtä datan kuvion vangitsemisessa, kun taas Cumulative Moving Average (CMA) jää huomattavasti jälkeen.
Go Further!
Onneksi olkoon, että olet suorittanut opetusohjelman loppuun.
Tämä opetusohjelma oli hyvä lähtökohta siihen, miten voit laskea datan liukuvat keskiarvot ja saada niistä tolkkua.
Kokeile kumulatiivisen ja eksponentiaalisen liukuvan keskiarvon python-koodin kirjoittamista ilman pandas-kirjastoa. Silloin saat paljon syvällisempää tietoa siitä, miten ne lasketaan ja millä tavoin ne eroavat toisistaan.
Tässä on vielä paljon kokeiltavaa. Kokeile laskea osittainen autokorrelaatio syötedatan ja liukuvan keskiarvon välillä ja yritä löytää jokin suhde näiden kahden välillä.
Jos haluat oppia lisää DataFrameista pandasissa, käy DataCampin interaktiivinen kurssi pandas Foundations.