Medias móviles en pandas

Introducción
Una media móvil, también llamada media rodante o corriente, se utiliza para analizar los datos de series temporales calculando las medias de diferentes subconjuntos del conjunto de datos completo. Dado que implica tomar la media del conjunto de datos a lo largo del tiempo, también se denomina media móvil (MM) o media rodante.
Hay varias formas de calcular la media rodante, pero una de ellas es tomar un subconjunto fijo de una serie completa de números. La primera media móvil se calcula promediando el primer subconjunto fijo de números, y luego se cambia el subconjunto avanzando al siguiente subconjunto fijo (incluyendo el valor futuro en el subgrupo mientras se excluye el número anterior de la serie).
La media móvil se utiliza sobre todo con datos de series temporales para capturar las fluctuaciones a corto plazo mientras se centra en las tendencias más largas.
Algunos ejemplos de datos de series temporales pueden ser los precios de las acciones, los informes meteorológicos, la calidad del aire, el producto interior bruto, el empleo, etc.
En general, la media móvil suaviza los datos.
La media móvil es la columna vertebral de muchos algoritmos, y uno de ellos es el modelo de media móvil integrada autorregresiva (ARIMA), que utiliza las medias móviles para hacer predicciones de datos de series temporales.
Hay varios tipos de medias móviles:
-
Media móvil simple (SMA): La media móvil simple (SMA) utiliza una ventana deslizante para tomar la media sobre un número determinado de períodos de tiempo. Es una media igualmente ponderada de los n datos anteriores.
Para entender mejor la SMA, tomemos un ejemplo, una secuencia de n valores:

entonces la media móvil igualmente ponderada para n puntos de datos será esencialmente la media de los M puntos de datos anteriores, donde M es el tamaño de la ventana móvil:

De manera similar, para calcular los valores sucesivos de la media móvil, se añadirá un nuevo valor a la suma, y el valor del período de tiempo anterior se descartará, ya que se tiene la media de los períodos de tiempo anteriores, por lo que no se requiere una suma completa cada vez:

- Media móvil acumulada (CMA): A diferencia de la media móvil simple, que elimina la observación más antigua a medida que se añade la nueva, la media móvil acumulativa tiene en cuenta todas las observaciones anteriores. La CMA no es una técnica muy buena para analizar tendencias y suavizar los datos. La razón es que promedia todos los datos anteriores hasta el punto de datos actual, por lo que es una media igualmente ponderada de la secuencia de n valores:



- Media móvil exponencial (EMA): A diferencia de la SMA y la CMA, la media móvil exponencial da más peso a los precios recientes y como resultado de ello, puede ser un mejor modelo o capturar mejor el movimiento de la tendencia de una manera más rápida. La reacción de EMA es directamente proporcional al patrón de los datos.
Dado que las EMAs dan un mayor peso a los datos recientes que a los datos más antiguos, son más sensibles a los últimos cambios de precios en comparación con las SMAs, lo que hace que los resultados de las EMAs sean más oportunos y por lo tanto las EMAs son más preferidas sobre otras técnicas.
Basta de teoría, ¿verdad? Saltemos a la implementación práctica de la media móvil.
Implementación de la media móvil en datos de series temporales
Media móvil simple (SMA)
Primero, vamos a crear datos de series temporales ficticias y a intentar implementar la SMA usando sólo Python.
Supongamos que hay una demanda de un producto y que se observa durante 12 meses (1 Año), y que necesita encontrar medias móviles para períodos de ventana de 3 y 4 meses.
Módulo de importación
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| mes | demanda | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Calculemos la SMA para un tamaño de ventana de 3, lo que significa que considerará tres valores cada vez para calcular la media móvil, y para cada nuevo valor, se ignorará el más antiguo.
Para implementar esto, utilizarás la función pandas iloc, ya que la columna demand es la que necesitas, fijarás la posición de esa en la función iloc mientras que la fila será una variable i que irás iterando hasta llegar al final del dataframe.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| mes | demanda | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Para comprobar la cordura, utilicemos también la función pandas incorporada rolling y veamos si coincide con nuestra media móvil simple personalizada basada en python.
df = df.iloc.rolling(window=3).mean()df.head()| mes | demanda | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, así que como puedes ver, las medias móviles personalizadas y las de pandas coinciden exactamente, lo que significa que tu implementación de la SMA era correcta.
Calculemos también rápidamente la media móvil simple para un window_size de 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| mes | demanda | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 2 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| mes | demanda | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299,3333 | 289,5 | 289,5 |
Ahora, trazarás los datos de las medias móviles que has calculado.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>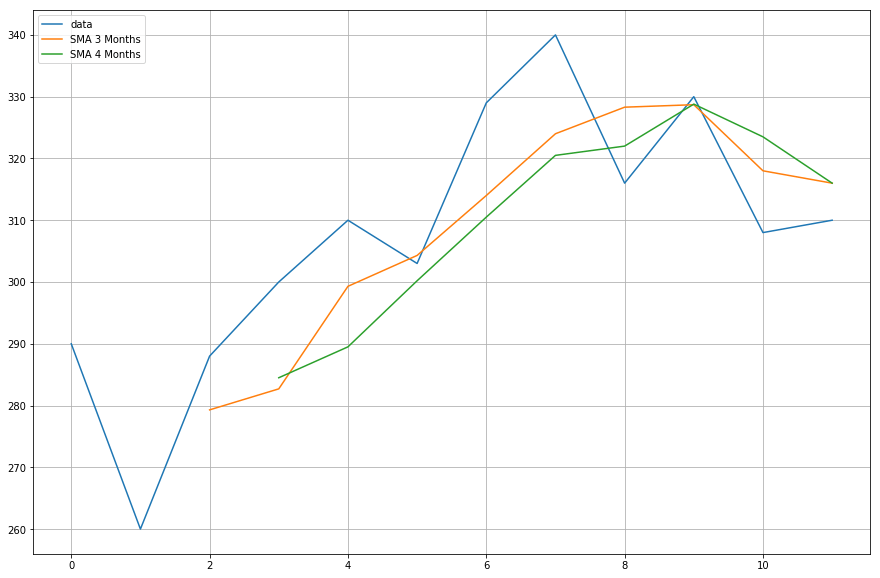
Media móvil acumulativa
Creo que ya estamos preparados para pasar a un conjunto de datos real.
Para la media móvil acumulativa, vamos a utilizar una air quality dataset que se puede descargar desde este enlace.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Fecha | Hora | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205,0 | 116,0 | 1490,0 | 1110,0 | 11,2 | 59,6 |
El preprocesamiento es un paso esencial siempre que se trabaja con datos. En el caso de los datos numéricos, uno de los pasos más comunes del preprocesamiento es la comprobación de los valores NaN (Null). Si hay algún valor NaN, se puede reemplazar por 0 o por la media o por los valores anteriores o posteriores o incluso eliminarlos. Aunque reemplazarlos es normalmente una mejor opción que eliminarlos, ya que este conjunto de datos tiene pocos valores NULL, eliminarlos no afectará a la continuidad de la serie.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64De la salida anterior, puede observar que hay alrededor de 114 valores NaN en todas las columnas, sin embargo, se dará cuenta de que están todos al final de la serie de tiempo, así que vamos a eliminarlos rápidamente.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Estará aplicando la media móvil acumulada en el Temperature column (T), así que separemos rápidamente esa columna de los datos completos.
df_T = pd.DataFrame(df.iloc)df_T.head()
Ahora, utilizarás el método pandas expanding para encontrar la media acumulada de los datos anteriores. Si recuerdas de la introducción, a diferencia de la media móvil simple, la media móvil acumulativa considera todos los valores anteriores al calcular la media.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Los datos de las series temporales se grafican con respecto al tiempo, así que vamos a combinar la columna de fecha y hora y convertirla en un objeto datetime. Para ello, utilizaremos el módulo datetime de python (Fuente: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Cambiemos el índice del dataframe temperature por el datetime.
df_T.index = df.DateTimeGraficemos ahora la temperatura real y la media móvil acumulada wrt. time.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Media móvil exponencial
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DateTime | |||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12,20 | 13,274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>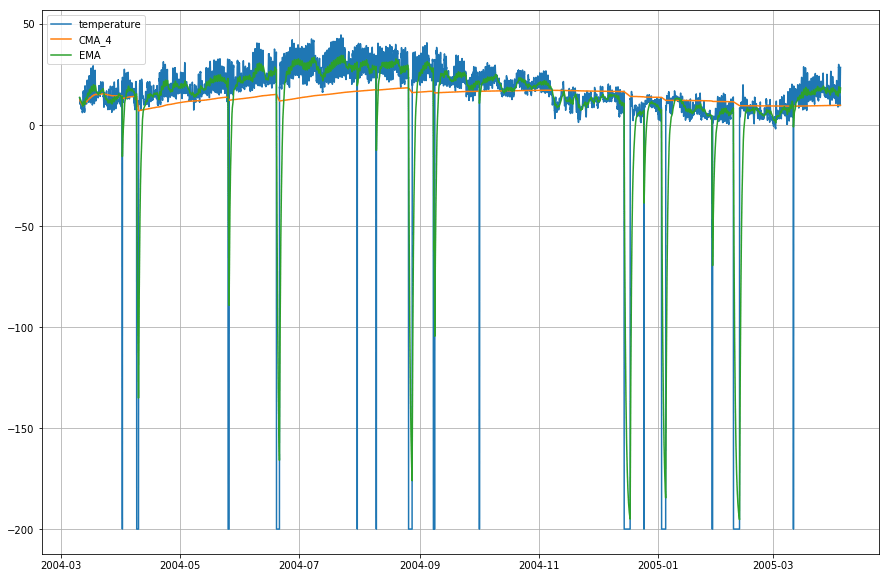
¡Vaya! Así que como se puede observar en el gráfico anterior, que el Exponential Moving Average (EMA) hace un trabajo magnífico en la captura del patrón de los datos, mientras que el Cumulative Moving Average (CMA) carece por un margen considerable.
¡Sigue adelante!
Felicidades por terminar el tutorial.
Este tutorial ha sido un buen punto de partida sobre cómo puedes calcular las medias móviles de tus datos y darle sentido.
Intenta escribir el código python de las medias móviles acumulativas y exponenciales sin usar la librería pandas. Eso te dará un conocimiento mucho más profundo sobre cómo se calculan y en qué se diferencian unas de otras.
Todavía hay mucho que experimentar. Intente calcular la autocorrelación parcial entre los datos de entrada y la media móvil, e intente encontrar alguna relación entre ambos.
Si quiere aprender más sobre DataFrames en pandas, tome el curso interactivo pandas Foundations de DataCamp.