El Desmultiplexor es un circuito combinacional que realiza la operación inversa del Multiplexor. Tiene una sola entrada, ‘n’ líneas de selección y un máximo de 2n salidas. La entrada se conectará a una de estas salidas en función de los valores de las líneas de selección.

Como hay ‘n’ líneas de selección, habrá 2n combinaciones posibles de ceros y unos. Por lo tanto, cada combinación puede seleccionar sólo una salida. El De-Multiplexor también se llama De-Mux.

1×4 De-Multiplexor

1×4 De-Multiplexor tiene una entrada I, dos líneas de selección, s1 & s0 y cuatro salidas Y3, Y2, Y1 &Y0. El diagrama de bloques de 1×4 De-Multiplexer se muestra en la siguiente figura.

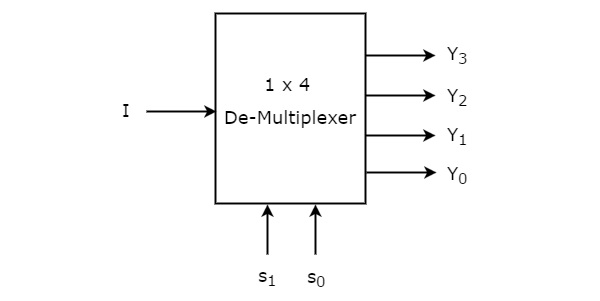
La única entrada ‘I’ se conectará a una de las cuatro salidas, Y3 a Y0 basado en los valores de las líneas de selección s1 & s0. La tabla de verdad del De-Multiplexor 1×4 se muestra a continuación.

Entradas de selección		Salidas
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	I
0	1	0	0	I	0
1	0	0	I	0	0
1	1	I	0	0	0

A partir de la tabla de verdad anterior, podemos escribir directamente las funciones booleanas para cada salida como

$Y_{3}=s_{1}s_{0}I$$

$Y_{2}=s_{1}{s_{0}’I$$

$$Y_{1}={s_{1}}’s_{0}I$$

$Y_{0}={s_1}'{s_{0}}’I$$

Podemos implementar estas funciones booleanas utilizando inversores & 3-puertas AND de entrada. El diagrama del circuito del De-Multiplexor 1×4 se muestra en la siguiente figura.

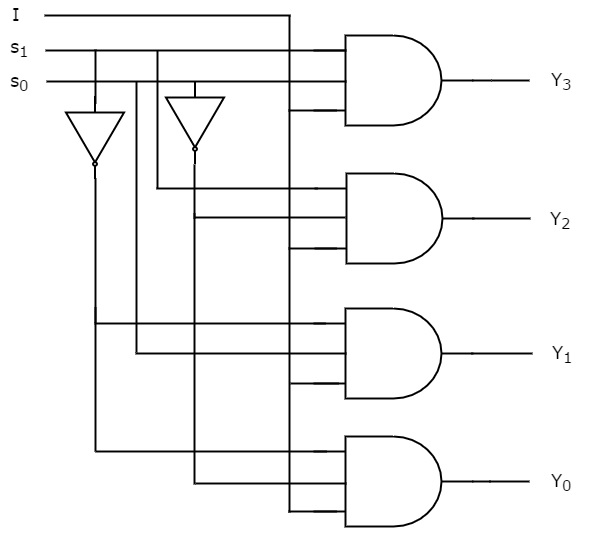
Podemos entender fácilmente el funcionamiento del circuito anterior. De forma similar, se puede implementar el Desmultiplexor de 1×8 y el Desmultiplexor de 1×16 siguiendo el mismo procedimiento.

Implementación de Desmultiplexores de orden superior

Ahora, implementemos los siguientes dos Desmultiplexores de orden superior utilizando Desmultiplexores de orden inferior.

• Desmultiplexor de 1×8
• Desmultiplexor de 1×16

Desmultiplexor de 1×8

En esta sección, vamos a implementar el Desmultiplexor de 1×8 utilizando Desmultiplexores de 1×4 y Desmultiplexor de 1×2. Sabemos que 1×4 De-Multiplexer tiene una sola entrada, dos líneas de selección y cuatro salidas. Mientras que, 1×8 De-Multiplexer tiene una sola entrada, tres líneas de selección y ocho salidas.

Así que, requerimos dos 1×4 De-Multiplexers en la segunda etapa con el fin de obtener las ocho salidas finales. Como el número de entradas en la segunda etapa es dos, necesitamos un DeMultiplexor 1×2 en la primera etapa para que las salidas de la primera etapa sean las entradas de la segunda. La entrada de este De-Multiplexor 1×2 será la entrada global del De-Multiplexor 1×8.

Dejemos que el De-Multiplexor 1×8 tenga una entrada I, tres líneas de selección s2, s1 & s0 y salidas Y7 a Y0. La tabla de verdad del De-Multiplexor 1×8 se muestra a continuación.

Entradas de selección			Salidas
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

Podemos implementar 1×8 De-Multiplexor utilizando Multiplexores de orden inferior fácilmente teniendo en cuenta la tabla de verdad anterior. El diagrama de bloques del De-Multiplexor 1×8 se muestra en la siguiente figura.

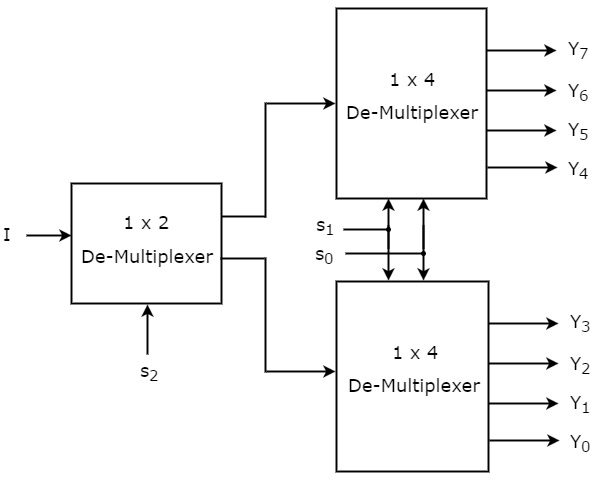
Las líneas de selección comunes, s1 & s0 se aplican a ambos De-Multiplexores 1×4. Las salidas del De-Multiplexor 1×4 superior son Y7 a Y4 y las salidas del De-Multiplexor 1×4 inferior son Y3 a Y0.

La otra línea de selección, s2 se aplica al De-Multiplexor 1×2. Si s2 es cero, entonces una de las cuatro salidas del Desmultiplexor 1×4 inferior será igual a la entrada, I basada en los valores de las líneas de selección s1 & s0. Del mismo modo, si s2 es uno, entonces una de las cuatro salidas del De-Multiplexor 1×4 superior será igual a la entrada, I basado en los valores de las líneas de selección s1 & s0.

De-Multiplexor 1×16

En esta sección, vamos a implementar el De-Multiplexor 1×16 utilizando De-Multiplexores 1×8 y De-Multiplexor 1×2. Sabemos que el De-Multiplexor 1×8 tiene una sola entrada, tres líneas de selección y ocho salidas. Mientras que, 1×16 De-Multiplexer tiene una sola entrada, cuatro líneas de selección y dieciséis salidas.

Entonces, requerimos dos 1×8 De-Multiplexers en la segunda etapa para obtener las dieciséis salidas finales. Como el número de entradas en la segunda etapa es dos, necesitamos un DeMultiplexor 1×2 en la primera etapa para que las salidas de la primera etapa sean las entradas de la segunda. La entrada de este De-Multiplexor 1×2 será la entrada global del De-Multiplexor 1×16.

Deja que el De-Multiplexor 1×16 tenga una entrada I, cuatro líneas de selección s3, s2, s1 & s0 y salidas Y15 a Y0. El diagrama de bloques del Desmultiplexor 1×16 utilizando Multiplexores de orden inferior se muestra en la siguiente figura.

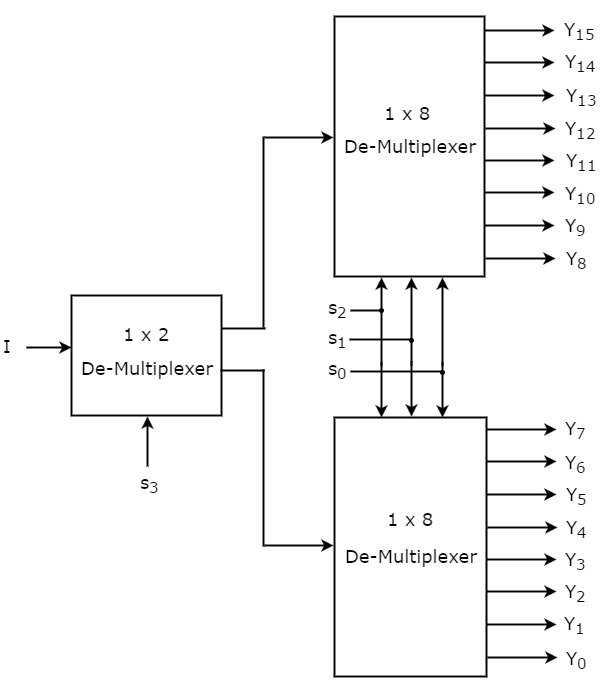
Las líneas de selección comunes s2, s1 & s0 se aplican a ambos Desmultiplexores 1×8. Las salidas del Desmultiplexor 1×8 superior son Y15 a Y8 y las salidas del Desmultiplexor 1×8 inferior son Y7 a Y0.

La otra línea de selección, s3 se aplica al De-Multiplexor 1×2. Si s3 es cero, entonces una de las ocho salidas del Desmultiplexor 1×8 inferior será igual a la entrada, I basada en los valores de las líneas de selección s2, s1 & s0. Del mismo modo, si s3 es uno, entonces una de las 8 salidas del De-Multiplexor 1×8 superior será igual a la entrada, I basada en los valores de las líneas de selección s2, s1 & s0.