De-Multiplexer ist eine kombinatorische Schaltung, die die umgekehrte Operation des Multiplexers durchführt. Er hat einen einzigen Eingang, ’n‘ Auswahlleitungen und maximal 2n Ausgänge. Der Eingang wird mit einem dieser Ausgänge auf der Grundlage der Werte der Auswahlleitungen verbunden.

Da es ’n‘ Auswahlleitungen gibt, gibt es 2n mögliche Kombinationen von Nullen und Einsen. Jede Kombination kann also nur einen Ausgang auswählen. De-Multiplexer wird auch als De-Mux bezeichnet.

1×4 De-Multiplexer

1×4 De-Multiplexer hat einen Eingang I, zwei Auswahlleitungen, s1 & s0 und vier Ausgänge Y3, Y2, Y1 &Y0. Das Blockdiagramm des 1×4 De-Multiplexers ist in der folgenden Abbildung dargestellt.

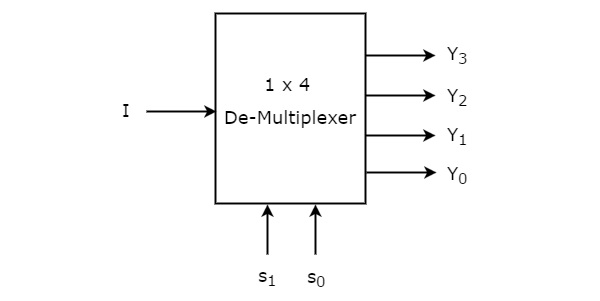
Der einzelne Eingang ‚I‘ wird mit einem der vier Ausgänge, Y3 bis Y0, verbunden, basierend auf den Werten der Auswahlleitungen s1 & s0. Die Wahrheitstabelle des 1×4 De-Multiplexers ist unten dargestellt.

Auswahl Eingänge		Ausgänge
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	I
0	1	0	0	I	0
1	0	0	I	0	0
1	1	I	0	0	0

Aus der obigen Wahrheitstabelle, können wir die booleschen Funktionen für jeden Ausgang direkt schreiben als

$$Y_{3}=s_{1}s_{0}I$$

$$$Y_{2}=s_{1}{s_{0}}’I$$

$$Y_{1}={s_{1}}’s_{0}I$$

$$$Y_{0}={s_1}'{s_{0}}’I$$

Wir können diese Booleschen Funktionen mit Hilfe von Invertern & 3-Eingangs-AND-Gatter. Der Schaltplan eines 1×4 De-Multiplexers ist in der folgenden Abbildung dargestellt.

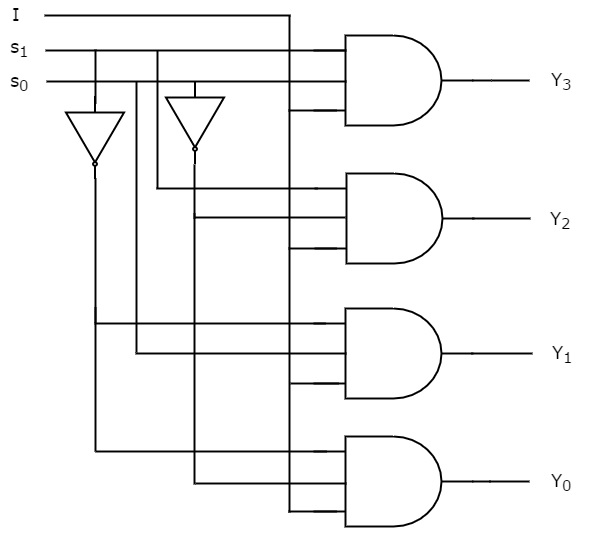
Wir können die Funktionsweise der obigen Schaltung leicht verstehen. In ähnlicher Weise kann man 1×8 De-Multiplexer und 1×16 De-Multiplexer implementieren, indem man das gleiche Verfahren anwendet.

Implementierung von De-Multiplexern höherer Ordnung

Nun wollen wir die folgenden zwei De-Multiplexer höherer Ordnung mit De-Multiplexern niedrigerer Ordnung implementieren.

• 1×8 De-Multiplexer
• 1×16 De-Multiplexer

1×8 De-Multiplexer

In diesem Abschnitt wollen wir 1×8 De-Multiplexer mit 1×4 De-Multiplexern und 1×2 De-Multiplexern implementieren. Wir wissen, dass 1×4 De-Multiplexer einen einzigen Eingang, zwei Auswahlleitungen und vier Ausgänge haben. Der 1×8 De-Multiplexer hingegen hat einen einzigen Eingang, drei Auswahlleitungen und acht Ausgänge.

Wir benötigen also zwei 1×4 De-Multiplexer in der zweiten Stufe, um die endgültigen acht Ausgänge zu erhalten. Da die Anzahl der Eingänge in der zweiten Stufe zwei ist, benötigen wir einen 1×2 De-Multiplexer in der ersten Stufe, so dass die Ausgänge der ersten Stufe die Eingänge der zweiten Stufe sind. Der Eingang dieses 1×2 De-Multiplexers wird der Gesamteingang des 1×8 De-Multiplexers sein.

Der 1×8 De-Multiplexer hat einen Eingang I, drei Auswahlleitungen s2, s1 & s0 und Ausgänge Y7 bis Y0. Die Wahrheitstabelle des 1×8 De-Multiplexers ist unten dargestellt.

Auswahl Eingänge			Ausgänge
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

Wir können den 1×8 De-Multiplexer mit Multiplexern niedrigerer Ordnung unter Berücksichtigung der obigen Wahrheitstabelle leicht implementieren. Das Blockdiagramm des 1×8 De-Multiplexers ist in der folgenden Abbildung dargestellt.

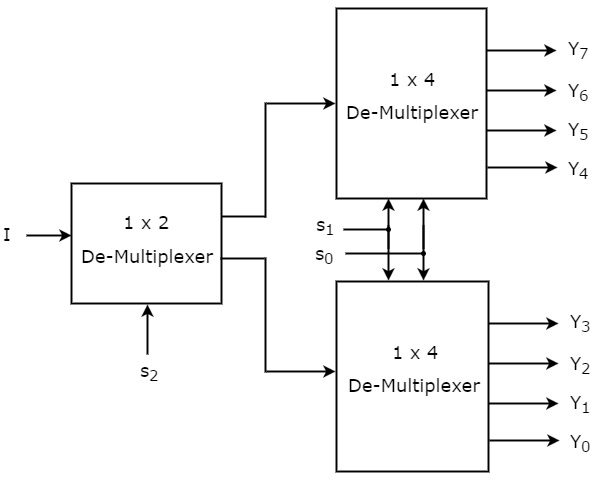
Die gemeinsamen Auswahlleitungen, s1 & s0 werden an beide 1×4 De-Multiplexer angelegt. Die Ausgänge des oberen 1×4-De-Multiplexers sind Y7 bis Y4 und die Ausgänge des unteren 1×4-De-Multiplexers sind Y3 bis Y0.

Die andere Auswahlleitung, s2, wird an den 1×2-De-Multiplexer angelegt. Wenn s2 gleich Null ist, dann ist einer der vier Ausgänge des unteren 1×4 De-Multiplexers gleich dem Eingang I, basierend auf den Werten der Auswahllinien s1 & s0. Wenn s2 gleich eins ist, dann ist einer der vier Ausgänge des oberen 1×4 De-Multiplexers gleich dem Eingang I, basierend auf den Werten der Auswahlzeilen s1 & s0.

1×16 De-Multiplexer

In diesem Abschnitt wollen wir einen 1×16 De-Multiplexer mit 1×8 De-Multiplexern und 1×2 De-Multiplexern implementieren. Wir wissen, dass 1×8 De-Multiplexer einen einzigen Eingang, drei Auswahlleitungen und acht Ausgänge haben. Der 1×16 De-Multiplexer hingegen hat einen einzigen Eingang, vier Auswahlleitungen und sechzehn Ausgänge.

Wir benötigen also zwei 1×8 De-Multiplexer in der zweiten Stufe, um die endgültigen sechzehn Ausgänge zu erhalten. Da die Anzahl der Eingänge in der zweiten Stufe zwei ist, benötigen wir einen 1×2 De-Multiplexer in der ersten Stufe, so dass die Ausgänge der ersten Stufe die Eingänge der zweiten Stufe sind. Der Eingang dieses 1×2 De-Multiplexers wird der Gesamteingang des 1×16 De-Multiplexers sein.

Der 1×16 De-Multiplexer hat einen Eingang I, vier Auswahlleitungen s3, s2, s1 & s0 und Ausgänge Y15 bis Y0. Das Blockdiagramm des 1×16 De-Multiplexers mit Multiplexern niedrigerer Ordnung ist in der folgenden Abbildung dargestellt.

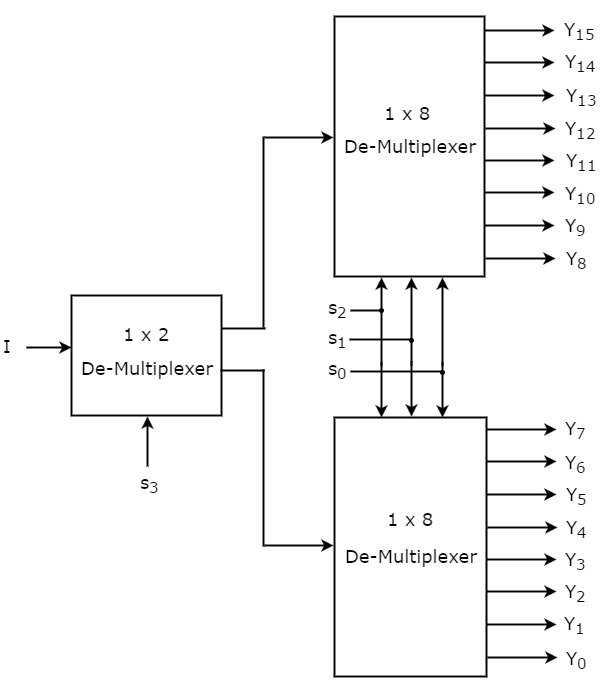
Die gemeinsamen Auswahlleitungen s2, s1 & s0 werden an beide 1×8 De-Multiplexer angelegt. Die Ausgänge des oberen 1×8 De-Multiplexers sind Y15 bis Y8 und die Ausgänge des unteren 1×8 DeMultiplexers sind Y7 bis Y0.

Die andere Auswahlleitung, s3, wird an den 1×2 De-Multiplexer angelegt. Ist s3 gleich Null, dann ist einer der acht Ausgänge des unteren 1×8 De-Multiplexers gleich dem Eingang I, basierend auf den Werten der Auswahlleitungen s2, s1 & s0. Wenn s3 gleich eins ist, entspricht einer der 8 Ausgänge des oberen 1×8 De-Multiplexers dem Eingang I auf der Grundlage der Werte der Auswahlzeilen s2, s1 & s0.