Glidende gennemsnit i pandas

Indledning
Et glidende gennemsnit, også kaldet et rullende eller løbende gennemsnit, bruges til at analysere tidsseriedata ved at beregne gennemsnit af forskellige delmængder af det komplette datasæt. Da det indebærer, at man tager gennemsnittet af datasættet over tid, kaldes det også for et glidende gennemsnit (MM) eller rullende gennemsnit.
Der er forskellige måder, hvorpå det rullende gennemsnit kan beregnes, men en af disse måder er at tage en fast delmængde fra en komplet talserie. Det første glidende gennemsnit beregnes ved at beregne gennemsnittet af den første faste delmængde af tal, og derefter ændres delmængden ved at bevæge sig fremad til den næste faste delmængde (herunder den fremtidige værdi i delmængden, mens det foregående tal udelukkes fra serien).
Det glidende gennemsnit anvendes for det meste med tidsseriedata for at opfange de kortsigtede udsving, mens der fokuseres på længere tendenser.
Et par eksempler på tidsseriedata kan være aktiekurser, vejrmeldinger, luftkvalitet, bruttonationalprodukt, beskæftigelse osv.
Generelt udglatter det glidende gennemsnit dataene.
Det glidende gennemsnit er en rygrad i mange algoritmer, og en af disse algoritmer er Autoregressive Integrated Moving Average Model (ARIMA), som bruger glidende gennemsnit til at foretage forudsigelser af tidsseriedata.
Der findes forskellige typer af glidende gennemsnit:
-
Simple Moving Average (SMA): Simple Moving Average (SMA):: Simple Moving Average (SMA) bruger et glidende vindue til at tage gennemsnittet over et fastsat antal tidsperioder. Det er et ligeligt vægtet gennemsnit af de foregående n data.
For at forstå SMA yderligere, lad os tage et eksempel, en sekvens af n værdier:

så vil det ligeligt vægtede glidende gennemsnit for n datapunkter i det væsentlige være gennemsnittet af de foregående M datapunkter, hvor M er størrelsen af det glidende vindue:

Sådan vil der ved beregning af efterfølgende rullende gennemsnitsværdier blive tilføjet en ny værdi til summen, og værdien for den foregående tidsperiode vil blive udeladt, da man har gennemsnittet af de foregående tidsperioder, så fuld summering hver gang er ikke nødvendig:

- Kumulativt glidende gennemsnit (CMA): I modsætning til det simple glidende gennemsnit, som fjerner den ældste observation, efterhånden som den nye bliver tilføjet, tager det kumulative glidende gennemsnit hensyn til alle tidligere observationer. CMA er ikke en særlig god teknik til analyse af tendenser og udjævning af data. Årsagen er, at den udregner gennemsnittet af alle de tidligere data frem til det aktuelle datapunkt, altså et ligevægtet gennemsnit af sekvensen af n værdier:



- Eksponentiel glidende gennemsnit (EMA): I modsætning til SMA og CMA giver eksponentiel glidende gennemsnit mere vægt til de seneste priser, og som følge heraf kan det være en bedre model eller bedre fange bevægelsen af tendensen på en hurtigere måde. EMA’s reaktion er direkte proportional med dataenes mønster.
Da EMA’er giver en højere vægt på nyere data end på ældre data, reagerer de mere på de seneste prisændringer sammenlignet med SMA’er, hvilket gør resultaterne fra EMA’er mere rettidige, og derfor er EMA mere at foretrække frem for andre teknikker.
Godt nok med teori, ikke? Lad os springe til den praktiske implementering af det glidende gennemsnit.
Implementering af glidende gennemsnit på tidsseriedata
Simple Moving Average (SMA)
Først skal vi oprette dummy tidsseriedata og prøve at implementere SMA ved hjælp af bare Python.
Antag, at der er en efterspørgsel efter et produkt, og det er observeret i 12 måneder (1 år), og du skal finde glidende gennemsnit for 3 og 4 måneders vinduesperioder.
Import module
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| month | efterspørgsel | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Lad os beregne SMA for en vinduesstørrelse på 3, hvilket betyder, at du vil overveje tre værdier hver gang for at beregne det glidende gennemsnit, og for hver ny værdi vil den ældste værdi blive ignoreret.
For at implementere dette vil du bruge pandas iloc-funktionen, da demand-kolonnen er det, du har brug for, vil du fastsætte positionen for den i iloc-funktionen, mens rækken vil være en variabel i, som du vil blive ved med at iterere, indtil du når slutningen af dataframeet.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| måned | efterspørgsel | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
For en sanity check, lad os også bruge den pandas indbyggede rolling funktion og se, om den stemmer overens med vores brugerdefinerede python-baserede simple glidende gennemsnit.
df = df.iloc.rolling(window=3).mean()df.head()| måned | efterspørgsel | SMA_3 | pandas_SMA_3 | ||
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | |
| 3 | 4 | 300 | 282.7 | 282.666667 | |
| 4 | 5 | 310 | 299.3 | 299.33333333 |
Cool, så som du kan se, passer de brugerdefinerede og pandas glidende gennemsnit nøjagtigt sammen, hvilket betyder, at din implementering af SMA var korrekt.
Lad os også hurtigt beregne det simple glidende gennemsnit for en window_size på 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| måned | efterspørgsel | SMA_3 | pandas_SMA_3 | SMA_4 | ||
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | |
| 1 | 2 | 260 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.33333333 | NaN | |
| 3 | 4 | 300 | 282.7 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| måned | efterspørgsel | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.33333333 | NaN | NaN | |
| 3 | 4 | 300 | 282.7 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.33333333 | 289.5 | 289.5 |
Nu skal du plotte dataene for de glidende gennemsnit, som du har beregnet.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>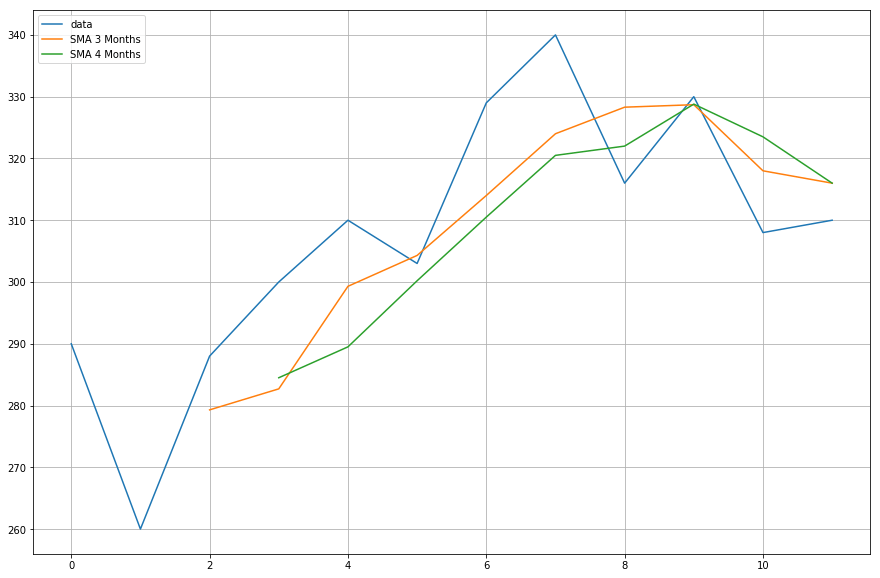
Kumulativt glidende gennemsnit
Jeg tror, at vi nu er klar til at gå over til et rigtigt datasæt.
Til kumulativt glidende gennemsnit skal vi bruge et air quality dataset, som kan downloades fra dette link.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Dato | Tid | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Forbehandling er et vigtigt skridt, når man arbejder med data. For numeriske data er et af de mest almindelige forbehandlingstrin at kontrollere, om der er NaN (Null)-værdier. Hvis der er NaN-værdier, kan du erstatte dem med enten 0 eller et gennemsnit eller forudgående eller efterfølgende værdier eller endog udelade dem. Selv om det normalt er et bedre valg at erstatte end at droppe dem, da dette datasæt har få NULL-værdier, vil det ikke påvirke seriens kontinuitet at droppe dem.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Fra ovenstående output kan du observere, at der er omkring 114 NaN-værdier på tværs af alle kolonner, men du vil dog finde ud af, at de alle er i slutningen af tidsserien, så lad os hurtigt droppe dem.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Du vil anvende kumulativt glidende gennemsnit på Temperature column (T), så lad os hurtigt adskille denne kolonne fra de komplette data.
df_T = pd.DataFrame(df.iloc)df_T.head()
Nu, skal du bruge pandas expanding-metoden til at finde det kumulative gennemsnit af de ovennævnte data. Hvis du husker fra indledningen, tager det kumulative glidende gennemsnit, i modsætning til det simple glidende gennemsnit, hensyn til alle de foregående værdier, når gennemsnittet beregnes.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Tidsseriedata plottes med hensyn til tiden, så lad os kombinere dato- og tidskolonnen og konvertere den til et datetime-objekt. For at opnå dette skal du bruge datetime modulet fra python (Kilde: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Lad os ændre indekset i temperature dataframe med datetime.
df_T.index = df.DateTimeLad os nu plotte den aktuelle temperatur og det kumulative glidende gennemsnit wrt. tid.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponentielt glidende gennemsnit
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |||
|---|---|---|---|---|---|
| DateTime | |||||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 | ||
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 | ||
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 | ||
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | ||
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>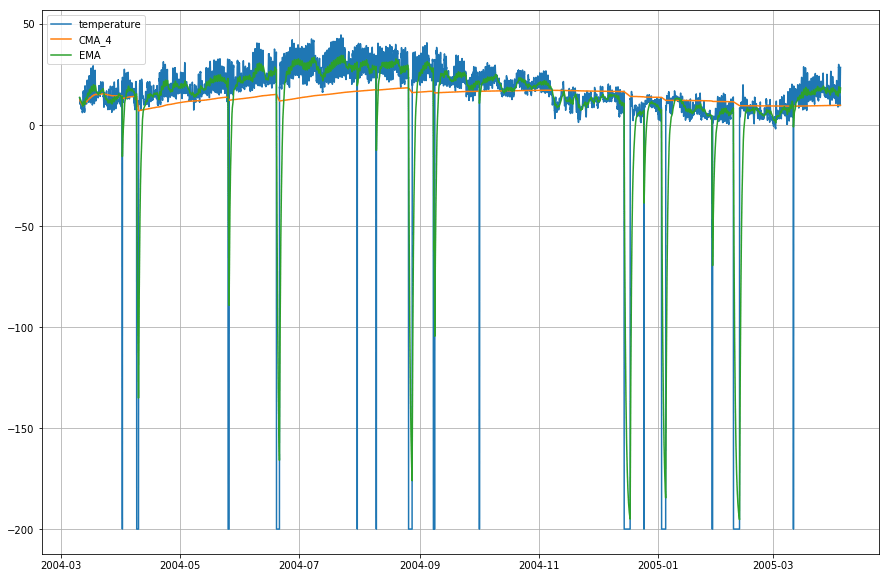
Wow! Så som du kan se af grafen ovenfor, at Exponential Moving Average (EMA) gør et fremragende stykke arbejde med at indfange mønstret i dataene, mens Cumulative Moving Average (CMA) mangler med en betydelig margen.
Gå videre!
Godt tillykke med at du har afsluttet denne tutorial.
Denne tutorial var et godt udgangspunkt for, hvordan du kan beregne de glidende gennemsnit af dine data og give mening med det.
Prøv at skrive den kumulative og eksponentielle glidende gennemsnit python-kode uden at bruge pandas-biblioteket. Det vil give dig en meget mere dybdegående viden om, hvordan de beregnes, og på hvilke måder de er forskellige fra hinanden.
Der er stadig meget at eksperimentere med. Prøv at beregne den delvise autokorrelation mellem inputdataene og det glidende gennemsnit, og prøv at finde en vis sammenhæng mellem de to.
Hvis du gerne vil lære mere om DataFrames i pandas, kan du tage DataCamps interaktive kursus Pandas Foundations.