Denne artikel blev oprindeligt offentliggjort på Cadence’s websted. Den er genoptrykt her med tilladelse fra Cadence.

Convolutional neural networks (CNN’er) anvendes i vid udstrækning til mønster- og billedgenkendelsesproblemer, da de har en række fordele i forhold til andre teknikker. Dette white paper dækker det grundlæggende om CNN’er, herunder en beskrivelse af de forskellige lag, der anvendes. Ved at bruge genkendelse af trafikskilte som eksempel diskuterer vi udfordringerne ved det generelle problem og introducerer algoritmer og implementeringssoftware udviklet af Cadence, som kan kompensere for beregningsbyrde og energi for en beskeden forringelse af genkendelsesprocenten for skilte. Vi skitserer udfordringerne ved at bruge CNN’er i indlejrede systemer og introducerer de vigtigste egenskaber ved Cadence® Tensilica® Vision P5 digital signalprocessor (DSP) for Imaging and Computer Vision og software, der gør den så velegnet til CNN-applikationer på tværs af mange billeddannelses- og relaterede genkendelsesopgaver.

Hvad er et CNN?

Et neuralt netværk er et system af sammenkoblede kunstige “neuroner”, der udveksler meddelelser mellem hinanden. Forbindelserne har numeriske vægte, der indstilles under træningsprocessen, således at et korrekt trænet netværk reagerer korrekt, når det præsenteres for et billede eller mønster, der skal genkendes. Netværket består af flere lag af “neuroner”, der registrerer funktioner. Hvert lag har mange neuroner, der reagerer på forskellige kombinationer af input fra de foregående lag. Som vist i figur 1 er lagene opbygget således, at det første lag registrerer et sæt primitive mønstre i input, det andet lag registrerer mønstre af mønstre, det tredje lag registrerer mønstre af disse mønstre og så videre. Typiske CNN’er anvender 5 til 25 forskellige lag til mønstergenkendelse.

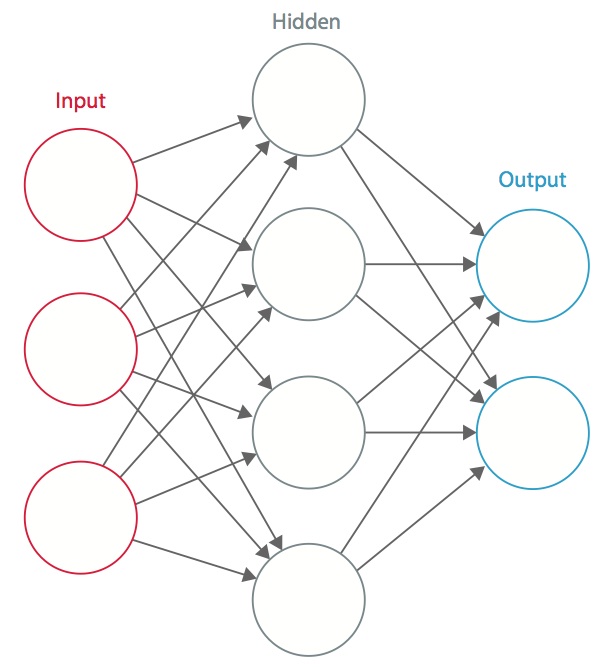
Figur 1: Et kunstigt neuralt netværk

Træning udføres ved hjælp af et “mærket” datasæt af input i et bredt udvalg af repræsentative inputmønstre, der er mærket med deres tilsigtede outputrespons. Ved træningen anvendes generelle metoder til iterativt at bestemme vægtene for mellemliggende og endelige funktionsneuroner. Figur 2 viser træningsprocessen på blokniveau.

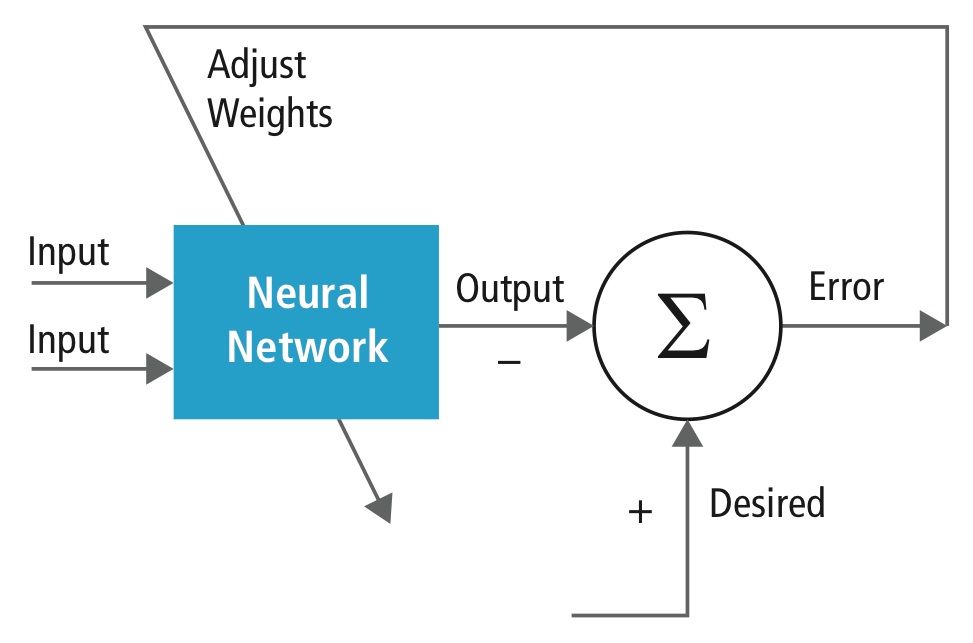
Figur 2: Træning af neurale netværk

Neurale netværk er inspireret af biologiske neurale systemer. Den grundlæggende beregningsenhed i hjernen er en neuron, og de er forbundet med synapser. Figur 3 sammenligner en biologisk neuron med en grundlæggende matematisk model.

Figur 3: Illustration af en biologisk neuron (øverst) og dens matematiske model (nederst)

I et virkeligt dyrisk nervesystem opfattes en neuron som en neuron, der modtager indgangssignaler fra sine dendritter og producerer udgangssignaler langs sin axon. Axonet forgrener sig og forbinder sig via synapser med dendritter fra andre neuroner. Når kombinationen af indgangssignaler når en vis tærskelbetingelse blandt dens indgangsdendritter, udløses neuronen, og dens aktivering kommunikeres til efterfølgende neuroner.

I den beregningsmæssige model for det neurale netværk interagerer de signaler, der bevæger sig langs axonerne (f.eks. x0), multiplikativt (f.eks. w0x0) med dendriterne på den anden neuron på grundlag af den synaptiske styrke ved den pågældende synapse (f.eks. w0). Synaptiske vægte kan læres og styrer den ene eller den anden neurons indflydelse. Dendriterne fører signalet videre til cellekroppen, hvor de alle summeres. Hvis den endelige sum er over en bestemt tærskelværdi, udløses neuronet og sender en spike langs sin akse. I beregningsmodellen antages det, at det præcise tidspunkt for affyringen er ligegyldigt, og at det kun er hyppigheden af affyringen, der overfører information. På grundlag af fortolkningen af frekvenskoden modelleres neuronets affyringshastighed med en aktiveringsfunktion ƒ, der repræsenterer frekvensen af spikes langs axonen. Et almindeligt valg af aktiveringsfunktion er sigmoidfunktionen. Kort sagt beregner hver neuron prikproduktet af input og vægte, tilføjer bias og anvender ikke-linearitet som en udløsningsfunktion (f.eks. efter en sigmoid responsfunktion).

Et CNN er et specialtilfælde af det neurale netværk, der er beskrevet ovenfor. Et CNN består af et eller flere konvolutionelle lag, ofte med et subsamplinglag, som efterfølges af et eller flere fuldt forbundne lag som i et standard neuralt netværk.

Designet af et CNN er motiveret af opdagelsen af en visuel mekanisme, den visuelle cortex, i hjernen. Den visuelle cortex indeholder en masse celler, der er ansvarlige for at detektere lys i små, overlappende underområder af synsfeltet, som kaldes receptive felter. Disse celler fungerer som lokale filtre over inputrummet, og de mere komplekse celler har større receptive felter. Foldningslaget i en CNN udfører den funktion, der udføres af cellerne i den visuelle cortex .

En typisk CNN til genkendelse af trafikskilte er vist i figur 4. Hver funktion i et lag modtager input fra et sæt funktioner, der er placeret i et lille kvarter i det foregående lag, kaldet et lokalt receptivt felt. Med lokale receptive felter kan funktioner udtrække elementære visuelle funktioner, såsom orienterede kanter, endepunkter, hjørner osv., som derefter kombineres af de højere lag.

I den traditionelle model for mønster-/ billedgenkendelse samler en hånddesignet funktionsekstraktor relevante infor- mationer fra input og eliminerer irrelevante variabiliteter. Ekstraktoren efterfølges af en trænbar klassifikator, et standard neuralt netværk, der klassificerer funktionsvektorer i klasser.

I et CNN spiller konvolutionslagene rollen som funktionsudtrækker. Men de er ikke designet i hånden. Konvolutionsfilterkernens vægte besluttes som en del af træningsprocessen. Foldningslagene er i stand til at udtrække de lokale træk, fordi de begrænser de skjulte lags receptive felter til at være lokale.

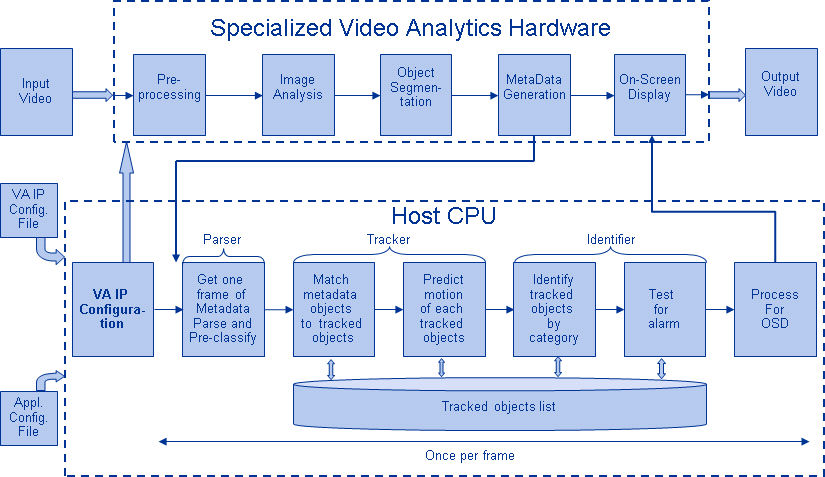
Figur 4: Typisk blokdiagram af en CNN

CNN’er anvendes inden for en række områder, herunder billed- og mønstergenkendelse, talegenkendelse, behandling af naturligt sprog og videoanalyse. Der er en række grunde til, at konvolutionelle neurale net bliver vigtige. I traditionelle modeller til mønstergenkendelse er feature extractors udformet i hånden. I CNN’er bestemmes vægtene i det konvolutionelle lag, der anvendes til ekstraktion af funktioner, og i det fuldt forbundne lag, der anvendes til klassificering, under træningsprocessen. De forbedrede netværksstrukturer i CNN’er fører til besparelser i hukommelseskrav og krav til beregningskompleksitet og giver samtidig bedre ydeevne for applikationer, hvor input har lokal korrelation (f.eks. billede og tale).

De store krav til beregningsressourcer til træning og evaluering af CNN’er opfyldes undertiden af grafikprocessorenheder (GPU’er), DSP’er eller andre siliciumarkitekturer, der er optimeret til høj gennemstrømning og lav energi ved udførelse af de idiosynkratiske mønstre i CNN-beregningen. Faktisk har avancerede processorer som Tensilica Vision P5 DSP for Imaging and Computer Vision fra Cadence et næsten ideelt sæt af beregnings- og hukommelsesressourcer, der er nødvendige for at køre CNN’er med høj effektivitet.

I mønster- og billedgenkendelsesapplikationer er de bedst mulige korrekte detektionsrater (CDR) blevet opnået ved hjælp af CNN’er. F.eks. har CNN’er opnået en CDR på 99,77 % ved hjælp af MNIST-databasen med håndskrevne tal , en CDR på 97,47 % med NORB-datasættet med 3D-objekter og en CDR på 97,6 % på ~5600 billeder af mere end 10 objekter . CNN’er giver ikke kun den bedste præstation sammenlignet med andre detektionsalgoritmer, de overgår endda mennesker i tilfælde som f.eks. klassificering af objekter i finkornede kategorier som f.eks. en bestemt hunderace eller fugleart .

Figur 5 viser en typisk vision-algoritme pipeline, som består af fire faser: forbehandling af billedet, detektering af interesseområder (ROI), der indeholder sandsynlige objekter, objektgenkendelse og beslutningstagning i forbindelse med vision. Forbehandlingsfasen er normalt afhængig af detaljerne i input, især kamerasystemet, og implementeres ofte i en fastforbundet enhed uden for vision-subsystemet. Beslutningstagningen i slutningen af pipelinen opererer typisk på genkendte objekter – den kan træffe komplekse beslutninger, men den opererer på langt færre data, så disse beslutninger er normalt ikke beregningsmæssigt svære eller hukommelseskrævende problemer. Den store udfordring ligger i objektsdetekterings- og genkendelsesfaserne, hvor CNN’er nu har stor indflydelse.

Figur 5: Vision-algoritme-pipeline

Lag af CNN’er

Gennem at stable flere og forskellige lag i en CNN opbygges komplekse arkitekturer til klassifikationsproblemer. Fire typer lag er mest almindelige: konvolutionslag, pooling/subsampling-lag, ikke-lineære lag og fuldt forbundne lag.

Konvolutionslag

Foldningsoperationen uddrager forskellige egenskaber ved input. Det første konvolutionslag uddrager egenskaber på lavt niveau som f.eks. kanter, linjer og hjørner. Lag på højere niveauer uddrager træk på højere niveauer. Figur 6 illustrerer den proces med 3D-foldning, der anvendes i CNN’er. Indgangen har størrelsen N x N x D og konvolveres med H kerner, der hver for sig har størrelsen k x k x D. Konvolution af et input med én kerne giver én udgangsfunktion, og med H kerner uafhængigt af hinanden giver H funktioner. Med udgangspunkt i inputets øverste venstre hjørne flyttes hver kerne fra venstre til højre, et element ad gangen. Når det øverste højre hjørne er nået, flyttes kernen et element nedad, og igen flyttes kernen fra venstre til højre, et element ad gangen. Denne proces gentages, indtil
kernen når det nederste højre hjørne. I det tilfælde, hvor N = 32 og k = 5 , er der 28 unikke positioner fra venstre til højre og 28 unikke positioner fra top til bund, som kernen kan indtage. I overensstemmelse med disse positioner vil hvert element i resultatet indeholde 28×28 (dvs. (N-k+1) x (N-k+1)) elementer. For hver position af kernen i en glidende vinduesproces multipliceres og akkumuleres k x k x k x D-elementer af input og k x k x D-elementer af kernen element-for-element. Så for at skabe et element af et output-feature er der behov for k x k x D multiplikations-akkumuleringsoperationer.

Figur 6: Billedlig fremstilling af konvolutionsprocessen

Pooling/subsampling lag

Pooling/subsampling laget reducerer opløsningen af funktionerne. Det gør funktionerne robuste over for støj og forvrængning. Der er to måder at foretage pooling på: max pooling og average pooling. I begge tilfælde opdeles input i ikke-overlappende todimensionale rum. I figur 4 er lag 2 f.eks. poolinglaget. Hver inputfunktion er på 28×28 og er opdelt i 14×14 regioner af størrelsen 2×2. Ved gennemsnitspooling beregnes gennemsnittet af de fire værdier i regionen. Ved max pooling vælges den maksimale værdi af de fire værdier.

Figur 7 uddyber poolingprocessen yderligere. Input er af størrelsen 4×4. Ved 2×2 subsampling opdeles et 4×4-billede i fire ikkeoverlappende matricer af størrelsen 2×2. I tilfælde af max pooling er den maksimale værdi af de fire værdier i 2×2-matricen output. I tilfælde af average pooling er gennemsnittet af de fire værdier output. Bemærk venligst, at for output med indeks (2,2) er resultatet af middelværdiberegningen en brøk, der er afrundet til nærmeste hele tal.

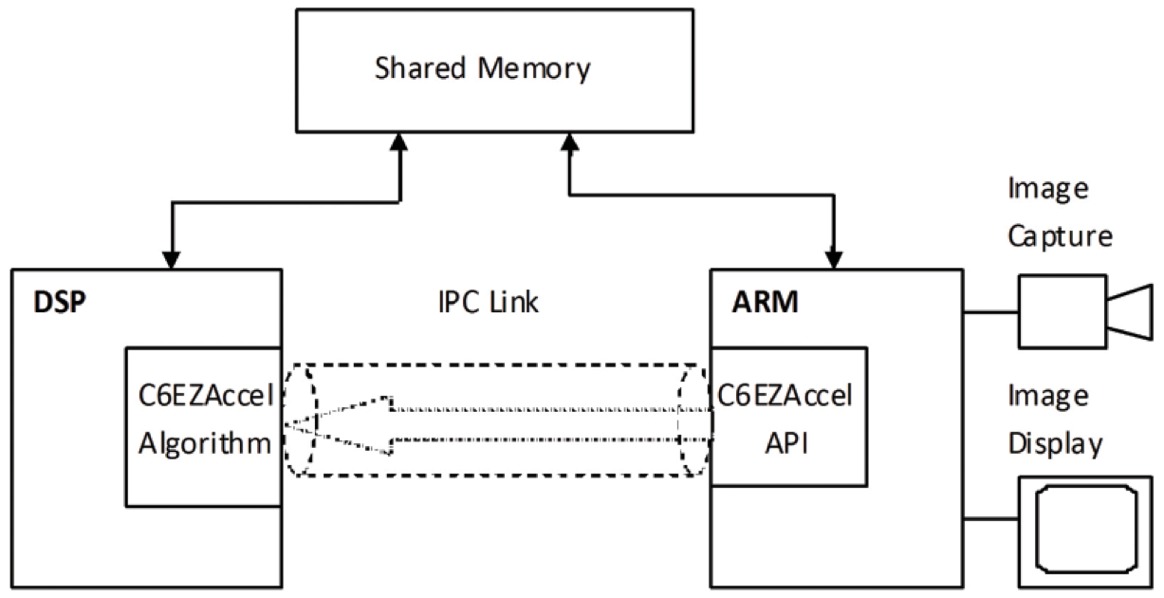
Figur 7: Billedlig fremstilling af max pooling og average pooling

Non-lineære lag

Neurale netværk i almindelighed og CNN’er i særdeleshed er afhængige af en ikke-lineær “trigger”-funktion til at signalere tydelig identifikation af sandsynlige træk på hvert skjult lag. CNN’er kan anvende en række specifikke funktioner – f.eks. rektificerede lineære enheder (ReLU’er) og kontinuerlige triggerfunktioner (ikke-lineære) – til effektivt at implementere denne ikke-lineære triggering.

ReLU

En ReLU implementerer funktionen y = max(x,0), så input- og outputstørrelserne i dette lag er de samme. Det øger de ikke-lineære egenskaber af beslutningsfunktionen og af det samlede netværk uden at påvirke receptive felter i konvolutionslaget. I sammenligning med de andre ikke-lineære funktioner, der anvendes i CNN’er (f.eks. hyperbolisk tangent, absolutte hyperbolisk tangent og sigmoid), er fordelen ved en ReLU, at netværket trænes mange gange hurtigere. ReLU-funktionen er illustreret i figur 8 med dens overførselsfunktion plottet over pilen.

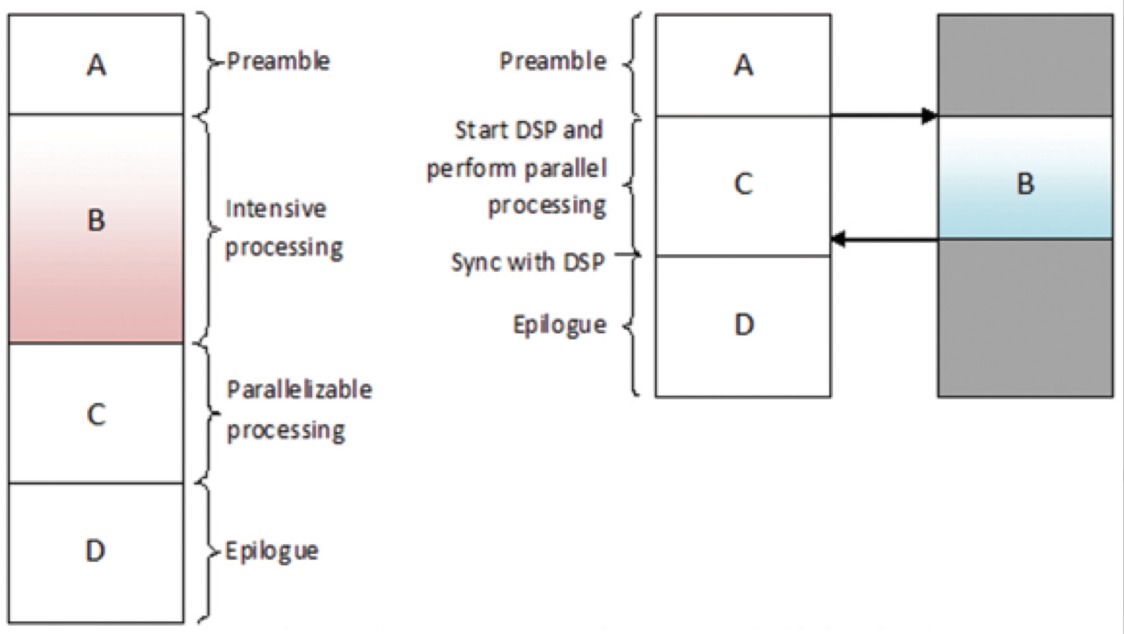
Figur 8: Billedlig fremstilling af ReLU-funktionen

Kontinuerlig triggerfunktion (ikke-lineær)

Det ikke-lineære lag opererer element for element i hver enkelt funktion. En kontinuerlig udløserfunktion kan være hyperbolisk tangent (figur 9), absolutte hyperbolisk tangent (figur 10) eller sigmoid (figur 11). Figur 12 viser, hvordan ikke-linearitet anvendes element for element.

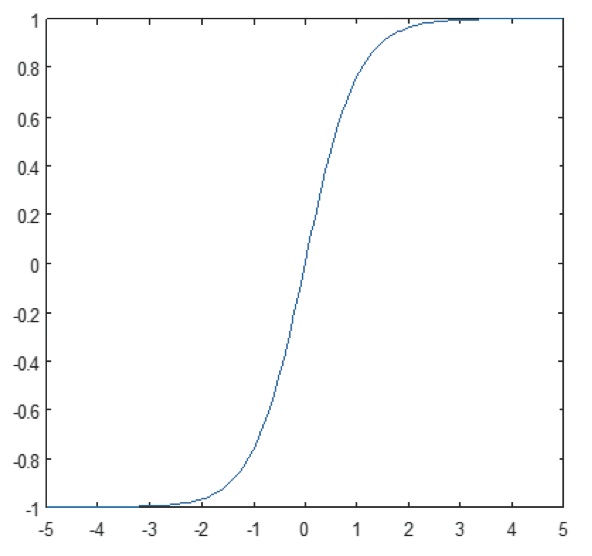
Figur 9: Plot af hyperbolisk tangentfunktion

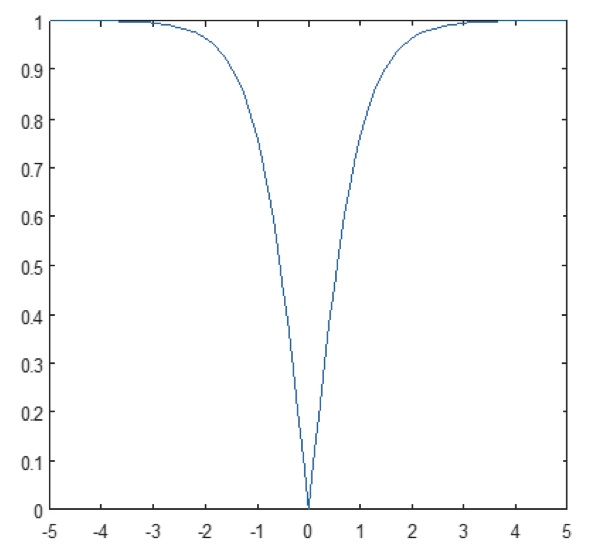
Figur 10: Plot af absolut af hyperbolisk tangentfunktion

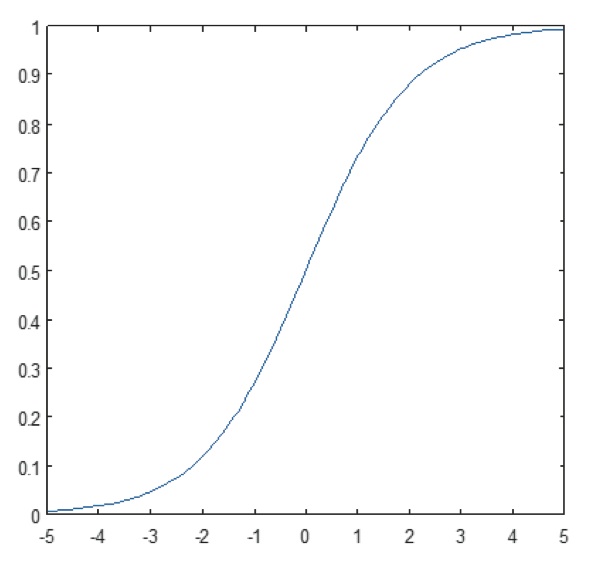
Figur 11: Plot af sigmoidfunktion

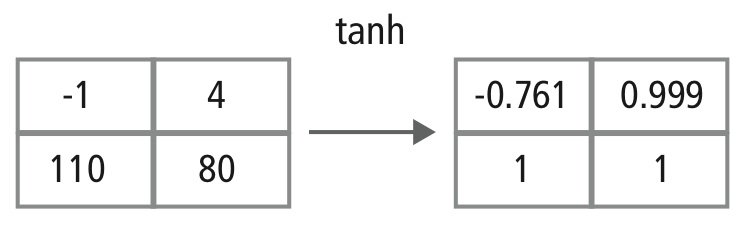
Figur 12: Billedlig fremstilling af tanh-behandling

Fuldt forbundne lag

Fuldt forbundne lag anvendes ofte som de sidste lag i en CNN. Disse lag opsummerer matematisk en vægtning af det foregående lag af funktioner, hvilket angiver den præcise blanding af “ingredienser” til bestemmelse af et specifikt måloutputresultat. I tilfælde af et fuldt forbundet lag bliver alle elementer af alle funktioner i det foregående lag anvendt i beregningen af hvert element af hver outputfunktion.

Figur 13 forklarer det fuldt forbundne lag L. Lag L-1 har to funktioner, som hver er 2×2, dvs. har fire elementer. Lag L har to funktioner, som hver har et enkelt element.

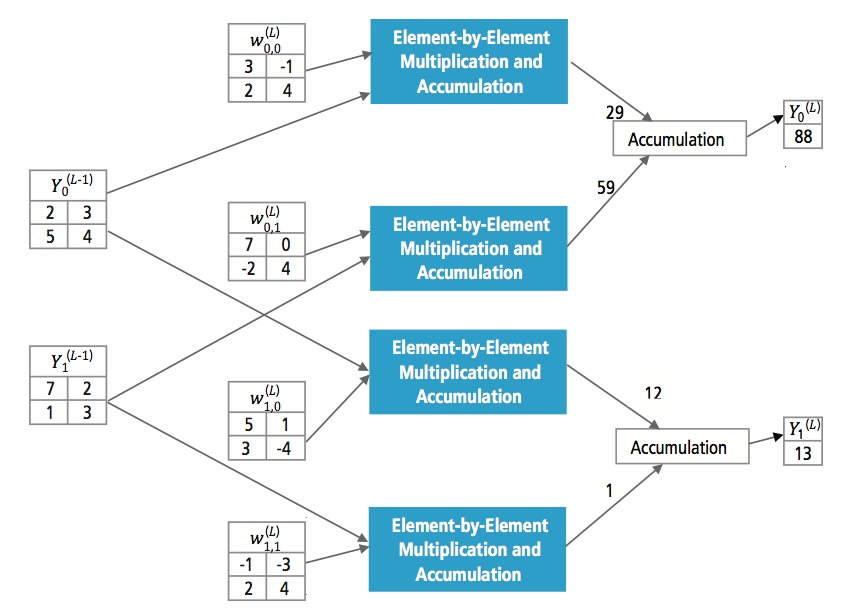
Figur 13: Behandling af et fuldt forbundet lag

Hvorfor CNN?

Mens neurale netværk og andre metoder til mønsterdetektion har eksisteret i de sidste 50 år, er der sket en betydelig udvikling på området for konvolutionelle neurale netværk i den seneste tid. Dette afsnit omhandler fordelene ved at bruge CNN til billedgenkendelse.

Robusthed over for forskydninger og forvrængninger i billedet

Detektion ved hjælp af CNN er robust over for forvrængninger som f.eks. formændringer på grund af kameralinsen, forskellige lysforhold, forskellige positurer, tilstedeværelse af delvis tildækning, horisontale og vertikale forskydninger osv. CNN’er er imidlertid uændrede i forhold til forskydninger, da den samme vægtkonfiguration anvendes i hele rummet. I teorien kan vi også opnå forskydningsinvari- antness ved hjælp af fuldt forbundne lag. Men resultatet af træningen i dette tilfælde er flere enheder med identiske vægtmønstre på forskellige steder i input. For at lære disse vægtkonfigurationer vil der være behov for et stort antal træningsinstanser for at dække rummet af mulige variationer.

Mindre hukommelseskrav

I det samme hypotetiske tilfælde, hvor vi bruger et fuldt forbundet lag til at udtrække funktionerne, vil et indgangsbillede på størrelse 32×32 og et skjult lag med 1000 funktioner kræve en størrelsesorden på 106 koefficienter, hvilket er et enormt hukommelseskrav. I det konvolutionelle lag anvendes de samme koefficienter på tværs af forskellige steder i rummet, så hukommelsesbehovet reduceres drastisk.

Enklere og bedre træning

Hvis man bruger det standard neurale netværk, der ville svare til et CNN, fordi antallet af param- etre ville være meget højere, ville træningstiden også stige forholdsmæssigt. I et CNN, da antallet af parametre er drastisk reduceret, reduceres træningstiden forholdsmæssigt. Under forudsætning af perfekt træning kan vi også designe et standard neuralt netværk, hvis ydeevne vil være den samme som et CNN. Men i praktisk træning ville
et standard neuralt netværk, der svarer til CNN, have flere parametre, hvilket ville føre til mere støjtilsætning under træningsprocessen. Derfor vil præstationen af et standard neuralt netværk, der svarer til et CNN, altid være dårligere.

Rekognitionsalgoritme til GTSRB-datasæt

The German Traffic Sign Recognition Benchmark (GTSRB) var en klassifikationsudfordring med flere klasser og et enkelt billede, der blev afholdt på International Joint Conference on Neural Networks (IJCNN) 2011, med følgende krav:

• 51 840 billeder af tyske vejskilte i 43 klasser (figur 14 og 15)
• Størrelsen af billederne varierer fra 15×15 til 222×193
• Billederne er grupperet efter klasse og spor med mindst 30 billeder pr. spor
• Billederne er tilgængelige som farvebilleder (RGB), HOG-features, Haar-features og farvehistogrammer
• Konkurrencen gælder kun klassifikationsalgoritmen; algoritme til at finde region af interesse i rammen er ikke påkrævet
• Temporal information i testsekvenserne deles ikke, så den temporale dimension kan ikke bruges i klassifikationsalgoritmen

Figur 14: GTSRB ideelle trafikskilte

Figur 15: GTSRB trafikskilte med forringelser

Cadence-algoritme til genkendelse af trafikskilte i GTSRB-datasæt

Cadence har udviklet forskellige algoritmer i MATLAB til genkendelse af trafikskilte ved hjælp af GTSRB-datasættet, startende med en baselinekonfiguration baseret på en velkendt artikel om skiltegenkendelse . Den korrekte detektionsrate på 99,24 % og en beregningsindsats på næsten >50 millioner multiplikator-adds pr. skilt er vist som et tykt grønt punkt i figur 16. Cadence har opnået væsentligt bedre resultater ved hjælp af vores nye proprietære hierarkiske CNN-tilgang. I denne algoritme er 43 trafikskilte blevet inddelt i fem familier. I alt implementerer vi seks mindre CNN’er. Den første CNN afgør, hvilken familie det modtagne trafikskilt hører til. Når skiltenes familie er kendt, køres den CNN (en af de resterende fem), der svarer til den fundne familie, for at afgøre, hvilket trafikskilt der hører til den pågældende familie. Ved hjælp af denne algoritme har Cadence opnået en korrekt detektionsrate på 99,58 %, hvilket er den bedste CDR, der hidtil er opnået på GTSRB.

Algoritme til afvejning af ydeevne vs. kompleksitet

For at kontrollere kompleksiteten af CNN’er i indlejrede applikationer har Cadence også udviklet en proprietær algoritme ved hjælp af egenværdi-dekomponering, der reducerer en trænet CNN til dens kanoniske dimension. Ved hjælp af denne algoritme har vi været i stand til at reducere kompleksiteten af CNN’en drastisk uden nogen form for ydelsesforringelse eller med en lille kontrolleret CDR-reduktion. Figur 16 viser de opnåede resultater:

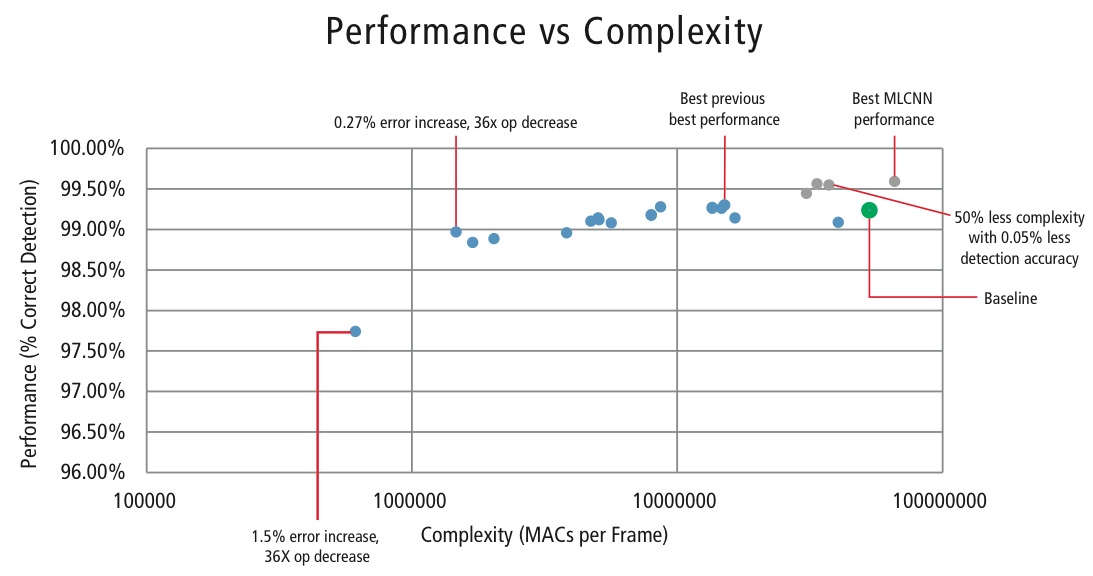
Figur 16: Plot over ydeevne vs. kompleksitet for forskellige CNN-konfigurationer til at detektere trafikskilte i GTSRB-datasættet

Det grønne punkt i figur 16 er baselinekonfigurationen. Denne konfiguration er ret tæt på den konfiguration, der er foreslået i Reference . Den kræver 53 MMAC’er pr. ramme for en fejlfrekvens på 0,76 %.

• Det andet punkt fra venstre kræver 1,47 millioner MAC’er pr. ramme for en fejlfrekvens på 1,03 %, dvs, for en stigning i fejlprocenten på 0,27% er MAC-kravet reduceret med en faktor 36,14.
• Det yderste punkt til venstre kræver 0,61 MMACs pr. ramme for at opnå en fejlprocent på 2,26%, dvs. antallet af MACs er reduceret med en faktor 86,4 gange.
• Punkterne med blå farve er for en CNN med et enkelt niveau, mens punkterne med rød farve er for en hierarkisk CNN. Den hierarkiske CNN opnår i bedste tilfælde en ydelse på 99,58 %.

CNN’er i indlejrede systemer

Som det fremgår af figur 5, kræver et visionsundersystem en masse billedbehandling ud over en CNN. For at kunne køre CNN’er på et strømbegrænset indlejret system, der understøtter billedbehandling, skal det opfylde følgende krav:

• Tilgængelighed af høj beregningspræstation: For en typisk CNN-implementering kræves der milliarder af MAC’er pr. sekund.
• Større belastnings-/lagringsbåndbredde: I tilfælde af et fuldt forbundet lag, der anvendes til klassifikationsformål, anvendes hver koefficient kun én gang til multiplikation. Så kravet til belastnings- og lagerbåndbredde er større end antallet af MAC’er, der udføres af processoren.
• Lavt dynamisk strømbehov: Systemet skal forbruge mindre strøm. For at løse dette problem er der behov for fastpunktsimplementering, hvilket stiller krav om at opfylde ydelseskravene ved hjælp af det mindst mulige antal bits.
• Fleksibilitet: Det skal være muligt let at opgradere det eksisterende design til et nyt design med bedre ydeevne.

Da beregningsressourcer altid er en begrænsning i indlejrede systemer, er det nyttigt at have en algoritme, der kan opnå store besparelser i beregningskompleksitet på bekostning af en kontrolleret lille forringelse af ydeevnen, hvis brugssituationen tillader en lille degra- dation i ydeevne, hvis det er muligt. Så Cadences arbejde med en algoritme til at opnå kompleksitet versus en afvejning af ydeevne, som forklaret i det foregående afsnit, har stor relevans for implementering af CNN’er på indlejrede systemer.

CNN’er på Tensilica-processorer

Tensilica Vision P5 DSP’en er en højtydende DSP med lavt strømforbrug, der er specielt designet til billed- og computervisionbehandling. DSP’en har en VLIW-arkitektur med SIMD-understøttelse. Den har fem udstedelsespladser i et instruktionsord på op til 96 bit og kan indlæse op til 1024-bit ord fra hukommelsen hver cyklus. Interne registre og operationsenheder spænder fra 512 bit til 1536 bit, hvor dataene repræsenteres som 16, 32 eller 64 skiver af 8b, 16b, 24b, 32b eller 48b pixeldata.

DSP’en tager fat på alle udfordringerne i forbindelse med implementering af CNN’er i indlejrede systemer, som beskrevet i det foregående afsnit.

• Adgang til høj beregningsydelse: Ud over den avancerede støtte til implementering af billedsignalbehandling har DSP’en instruktionsstøtte til alle trin af CNN’er. Til konvolutionsoperationer har den et meget rigt instruktionssæt, der understøtter multiplikation/multiplikation-akkumulering af operationer, der understøtter 8b x 8b, 8b x 16b og 16b x 16b operationer for underskrevne/uunderskrevne data. Den kan udføre op til 64 8b x 16b og 8b x 8b multiplikations-/multiplikations-akkumuleringsoperationer i en cyklus og 32 16b x 16b multiplikations-/multiplikations-akkumuleringsoperationer i en cyklus. Med henblik på maksimal pooling og ReLU-funktionalitet har DSP’en instruktioner til at foretage 64 8-bit sammenligninger i en cyklus. Til implementering af ikke-lineære funktioner med begrænsede intervaller som tanh og signum har den instruktioner til at implementere en opslagstabel for 64 7-bit værdier i én cyklus. I de fleste tilfælde bliver instruktionerne til sammenligning og opslagstabel planlagt parallelt med multiplikations-/multiplikations-akkumuleringsinstruktionerne og tager ikke ekstra cyklusser.
• Større load/store-båndbredde: DSP’en kan udføre op til to 512-bit load/store-operationer pr. cyklus.
• Lavt dynamisk strømforbrug: DSP’en er en fixed-point-maskine. På grund af den fleksible håndtering af en række forskellige datatyper kan der opnås fuld ydeevne og energifordel ved blandet 16b- og 8b-beregning med et minimalt tab af nøjagtighed.
• Fleksibilitet: Da DSP’en er en programmerbar processor, kan systemet opgraderes til en ny version blot ved at foretage en firmwareopgradering.
• Floating Point: Til algoritmer, der kræver et udvidet dynamisk område for deres data og/eller koefficienter, har DSP’en en valgfri vektor-flydepunktsenhed.

Vision P5 DSP’en leveres med et komplet sæt softwareværktøjer, der omfatter en højtydende C/C++-kompiler med automatisk vektorisering og planlægning til understøttelse af SIMD- og VLIW-arkitekturen uden behov for at skrive assembler-sprog. Dette omfattende værktøjssæt omfatter også linker, assembler, debugger, profiler og grafiske visualiseringsværktøjer. En omfattende instruktionssæt-simulator (ISS) giver designeren mulighed for hurtigt at simulere og evaluere ydeevnen. Når der arbejdes med store systemer eller lange testvektorer, opnår den hurtige, funktionelle TurboXim-simulatoroption hastigheder, der er 40X til 80X hurtigere end ISS med henblik på effektiv softwareudvikling og funktionel verifikation.

Cadence har implementeret en CNN-arkitektur med et enkelt lag på DSP’en til genkendelse af tyske trafikskilte. Cadence har opnået en CDR på 99,403 % med 16-bit kvantisering for dataeksempler og 8-bit kvantisering for koefficienter i alle lag for denne arkitektur. Den har to konvolutionslag, tre fuldt forbundne lag, fire ReLU-lag, tre max pooling-lag og et ikke-lineært tanh-lag. Cadence har opnået en gennemsnitlig ydelse på 38,58 MACs/cyklus for det komplette netværk, herunder cyklusser for alle max pooling-, tanh- og ReLU-lagene. Cadence har i bedste fald opnået en ydelse på 58,43 MACs pr. cyklus for det tredje lag, herunder cyklusser for tanh- og ReLU-funktionaliteterne. Denne DSP, der kører ved 600 MHz, kan behandle mere end 850 trafikskilte på et sekund.

Fremtiden for CNN’er

Af de lovende områder inden for forskningen i neurale netværk er recurrent neural networks (RNN’er), der anvender long short- term memory (LSTM). Disse områder leverer det nuværende tekniske niveau inden for tidsseriegenkendelsesopgaver som f.eks. talegenkendelse og håndskriftgenkendelse. RNN/autoenkodere er også i stand til at generere håndskrift/tale/billeder med en kendt fordeling ,,,,.

Deep belief networks, en anden lovende netværkstype, der anvender restricted Boltzman machines (RMB’er)/autoenkodere, kan trænes grådigt, et lag ad gangen, og er derfor lettere at træne til meget dybe netværk ,.

Slutning

CNNN’er giver de bedste resultater i forbindelse med mønster-/billedgenkendelsesproblemer og klarer sig endda bedre end mennesker i visse tilfælde. Cadence har opnået de bedste resultater i branchen ved hjælp af proprietære algoritmer og arkitekturer med CNN’er. Vi har udviklet hierarkiske CNN’er til genkendelse af trafikskilte i GTSRB og har opnået den bedste præstation nogensinde på dette datasæt. Vi har udviklet en anden algoritme til afvejning af ydeevne mod kompleksitet og har været i stand til at opnå en kompleksitetsreduktion med en faktor 86 for en CDR-forringelse på mindre end 2 %. Tensilica Vision P5 DSP til billeddannelse og computervision fra Cadence har alle de funktioner, der er nødvendige for at implementere CNN’er ud over de funktioner, der er nødvendige for at foretage billedsignalbehandling. Der kan udføres mere end 850 genkendelser af trafikskilte ved at køre DSP’en ved 600 MHz. Tensilica Vision P5 DSP fra Cadence har et næsten ideelt sæt funktioner til at køre CNN’er.

“Artificial neural network.” Wikipedia. https://en.wikipedia.org/wiki/Artificial_neural_network

Karpathy, Andrej. 2015. “Neurale netværk del 1: Opsætning af arkitekturen”. Noter til CS231n Convolutional Neural Networks for Visual Recognition, Stanford University. http://cs231n.github.io/neural-networks-1/

“Convolutional neural network.” Wikipedia. https://en.wikipedia.org/wiki/Convolutional_neural_network

Sermanet, Pierre, og Yann LeCun. 2011. “Traffic Sign Recognition with Multi Scale Networks.” Courant Institute of Mathematical Sciences, New York University. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6033589

Ciresan, Dan, Ueli Meier og Jürgen Schmidhuber. 2012. “Multi-column deep neural networks for image classi- fication.” 2012 IEEE Conference on Computer Vision and Pattern Recognition (2012 IEEE Conference on Computer Vision and Pattern Recognition (New York, NY: Institute of Electrical and Electronics Engineers (IEEE)). http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6248110

Ciresan, Dan, Ueli Meier, Jonathan Masci, Luca M. Gambardella og Jurgen Schmidhuber. 2011. “Fleksible, højtydende konvolutionelle neurale netværk til billedklassifikation”. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence-Volume Two: 1237-1242. Hentet den 17. november 2013. http://people.idsia.ch/~juergen/ijcai2011.pdf

Lawrence, Steve, C. Lee Giles, Ah Chung Tsoi, og Andrew D. Back. 1997. “Face Recognition: A Convolutional Neural Network Approach.” IEEE Transactions on Neural Networks, Volume 8; Issue 1. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=554195

Russakovsky, O. et al. 2014. “ImageNet Large Scale Visual Recognition Challenge”. International Journal of Computer Vision. http://link.springer.com/article/10.1007/s11263-015-0816-y#

Ovtcharov, Kalin, Olatunji Ruwarse, Joo-Young Kim et al. 22. feb. 2015. “Accelerating Deep Convolutional Networks Using Specialized Hardware”. Microsoft Research. http://research-srv.microsoft.com/pubs/240715/CNN%20Whitepaper.pdf

Stallkamp, J., M. Schlipsing, J. Salmen, og C. Igel. “Man Vs. Computer: Benchmarking Machine Learning Algorithms For Traffic Sign Application.” IJCNN 2011. http://www.sciencedirect.com/science/article/pii/S0893608012000457

Hochreiter, Sepp, og Jürgen Schmidhuber. 1997. “Long Short-Term Memory.” Neural Computation, 9(8):1735-1780. ftp://ftp.idsia.ch/pub/juergen/lstm.pdf

Graves, Alex. 2014. “Generating Sequences With Recurrent Neural Networks.” http://arxiv.org/abs/1308.0850

Schmidhuber, Jurgen. 2015. “Recurrent Neural Networks.” http://people.idsia.ch/~juergen/rnn.html

Olshausen, Bruno A., og David J. Field. 1996. “Fremkomst af receptive feltegenskaber for simple celler ved indlæring af en sparsom kode for naturlige billeder.” Nature 381.6583: 607-609. http://www.nature.com/nature/journal/v381/n6583/abs/381607a0.html

Hinton, G. E. og Salakhutdinov, R. R. 2006. “Reduktion af dataenes dimensionalitet med neurale netværk”. Science vol. 313 no. 5786 pp. 504-507. http://www.sciencemag.org/content/suppl/2006/08/04/313.5786.504.DC1.

Hinton, Geoffrey E. 2009. “Deep belief networks.” Scholarpedia, 4(5):5947.
http://www.scholarpedia.org/article/Deep_belief_networks